Я знаю сам, что это - не игра..

В.Шаламов

Геометрическое моделирование форм объектов живой природы относится к важнейшему разделу архитектурной бионики. В фундаментальной работе Ю.С.Лебедева (1) приводится большое количество геометрических моделей более или менее точно отражающих формы различных природных структур. В теоретическом плане природные спиральные структуры интересны еще и тем, что они связаны с таким явлением как филлотаксис (расположение семян, листьев, чешуек), что, в свою очередь, связано с изучением, широко известной в архитектуроведении и искусствоведении, пропорции «золотого сечения». Научное изучение филлотаксиса началось достаточно давно. В частности, еще в 1754 году швейцарский натуралист Шарль Бонне высказал предположение, что листья на стволе распределяются так, чтобы как можно меньше закрывать друг друга. В этом случае они лучше освещаются солнечными лучами и омываются дождём. А в корзинке подсолнуха семечки располагаются так, что между ними образуется минимальное количество пустот.

В природе спиральные структуры имеют устойчивую и очевидную закономерность - количество правых и левых спиралей неодинаково и их соотношение является близким к иррациональной пропорции «золотого сечения». Почему природа «выбрала» именно эту пропорцию пока не совсем ясно. В работе (2) приводится математическая модель, показывающая как наиболее эффективно заполнить корзинку подсолнуха зёрнами путем последовательного деления окружности секторами определенного угла. Аналитическое решение такой задачи дает угол равный части окружности, соотносящейся с ней в пропорции «золотого сечения». При этом, нет пока ясности, как соотносится «эффективное деление» окружности на сектора с минимизацией пустот между семечками.

Попытаемся сформулировать и решить задачу на поиск экстремума. Построение спиральных структур основывается на следующей геометрической модели. Имеется центр спирали «С». Первая точка или узел (в ботанике их принято называть примордиями) спирали отступает от него на расстояние квадратного корня из одного.  Вторая точка - квадратного корня из двух. Третья - квадратного корня из трех. И так далее (рис.1).

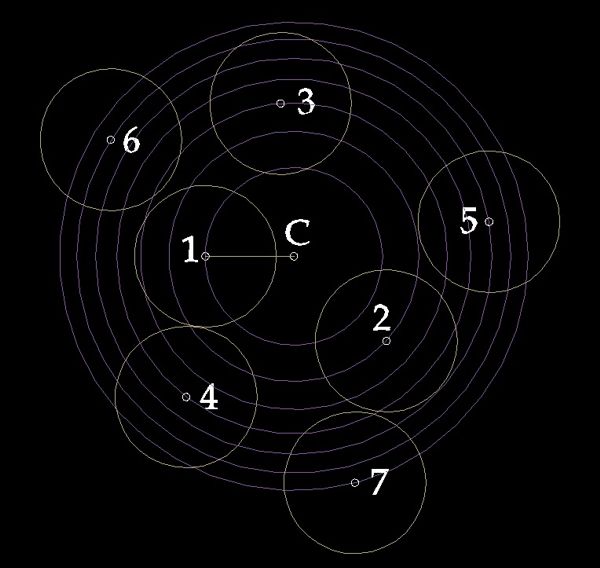
Множество точек образуют линию похожую на спираль Ферма. Все точки задаются с одинаковым поворотом, который называется углом дивергенции. Считается что при угле дивергенции, равном 137,5 градусам (результат примерного деления полной длины окружности на «золотое сечение») получается спиральная структура тождественная раскладке семечек в подсолнухе (рис.). 

Подсолнух растущий и подсолнух зрелый - разные модели, разные спирали. 

Рис.1. Сетка + подсолнух

Для поиска экстремума, нами была составлена программа геометрического построения спиралей с углом дивергенции от 0  до 180 градусов с шагом 0,01 градуса (всего 18 000 вариантов). Программа была написана в программе Rhino Grasshopper. Количество точек - узлов спиралей для удобства визуального восприятия было принято равным 700. Полный набор полученных изображений был записан в виде видеоролика. В качестве критерия поиска экстремума было выбрано минимальное расстояние между узлами спирали. В автоматизированном режиме была построена сетка Воронова (рис...). В этом случае учитываются расстояния между ближайшими точками - узлами спирали. Таких ближайших точек может быть 5 или 6 (рис....). Для оптимизации задачи в алгоритм построения спирали было заложено ограничение количества ближайших точек - не более двух. В этом случае получается очень интересное геометрическое построение спиральных структур - в виде ветвлений. При этом, в соответствии с количеством правых и левых ветвлений, получаются определенные числовые ряды, свойства которых будут рассмотрены далее. В автоматизированном режиме был сделан перебор 18 000 вариантов спиральных структур на предмет выявления тех вариантов, в которых расстояния между точками получается максимальным (табл.1).

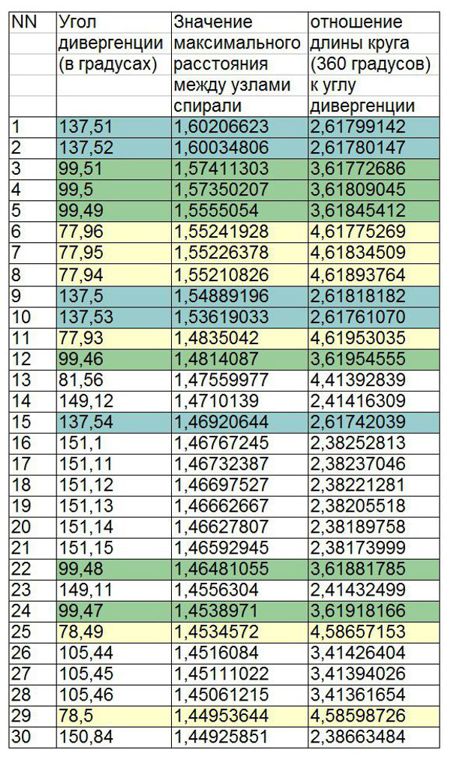
Результаты показали, что экстремальное значение получается при угле дивергенции 137,51 градуса, т.е. при угле «золотого сечения» (360/(1+Ф)). Кроме того, результаты, близкие к экстремальному получились при других «золотых» углах - 99,51 градуса (360/(2+Ф)), 77,96 градуса (360/3+Ф)).  Любопытно, что в группе «лидеров» оказались углы, которые можно трактовать как производные от корня квадратного 149,11 градусов (360/(1+scrt2)), 105,45 градусов (360/(2+scrt2)),  81,56 градусов  (360/(2+scrt2)). 

Любопытно, что получились большие расстояния при угле дивергенции в 151,11 градусов. Коэффициент 2,382 можно трактовать двояко. Это может быть значение близкое к 2,414 = (1+scrt2). А можно трактовать как 2,382 = 4-Ф.

Минимальные расстояния получились при углах дивергенции, которые относятся к полной окружности в целочисленно-кратном соотношении - 180 градусов (½ окружности), 120 градусов (¼ окружности) и т.д. (табл.2)

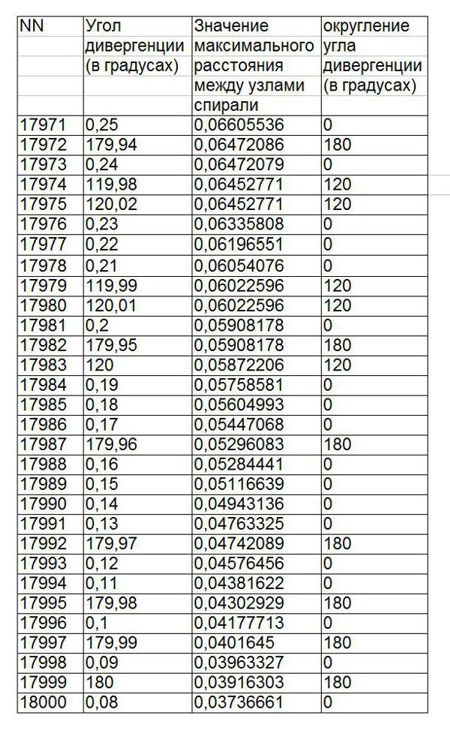
При построении спиралей с каким-либо заданным углом дивергенции, можно заметить, что расстояния между узлами не являются одинаковыми. Если угол дивергенции является величиной кратной 360 градусам, то минимальные расстояния между узлами можно наблюдать на периферии спирали, как правило, между последним и предпоследним узлами (рис...).

В этом случае разница между минимальным и максимальным расстояниями оказывается весьма значительной. Например, при нулевом угле дивергенции, расстояние между первым и вторым узлами равно 0,4142 (scrt2 - scrt1). А расстояния между последним и предпоследним узла, если допустить, что количество узлов равно 200, будет равно  0,0189  (scrt200 - scrt199). Первое значение получается больше второго почти в 12 раз. Подобное соотношение в спирали с углом дивергенции, равным 137,51 градуса, составляет всего  1,1182.

Проведенная нами проверка показала, что по критерию разницы между максимальным и минимальным расстояниями между узлами спирали, «золотой» угол также является предельным (табл.3).

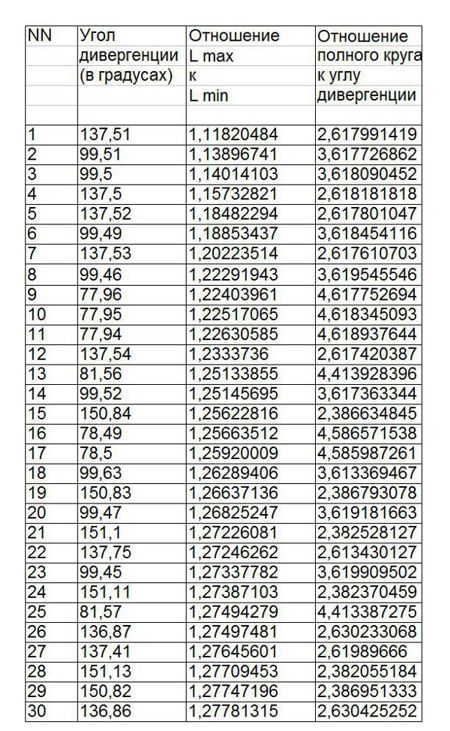
В этой минимальной разнице между расстояниями между узлами заключается еще один экстремум «золотого» угла. Расстояния между узлами являются не только максимально возможными, но они еще почти одинаковы. Получается предельно оптимально-равномерное распределение узлов спирали в плоскости круга.     

Поскольку узлы спирали равномерно равноудалены друг от друга, то на месте узлов можно расположить некие подобные геометрические фигуры с суммарной площадью максимально превышающей площадь пустот между ними. Такими фигурами может быть круг или квадрат (рис...).

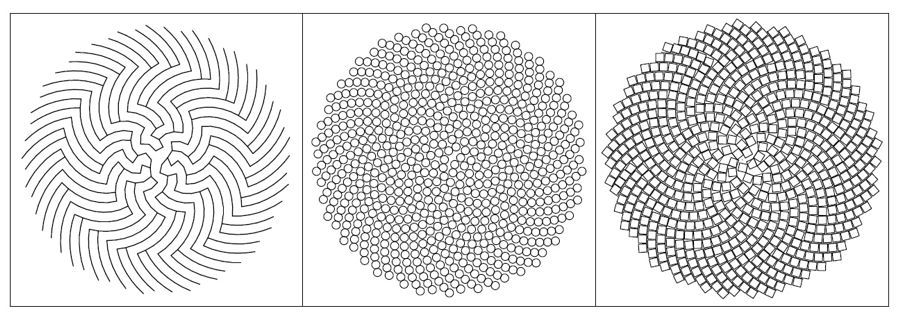
Если в качестве такой фигуры использовать окружность или шар, то можно получить модель, очень похожую на корзинки некоторых природных объектов (подсолнухи, маргаритки и др.).

Очевидно, что геометрическое построение формы семечек в подсолнухе отличается от построения цветков, имеющих форму близкую к кругу. Если в каждом узле построить окружность, то с увеличением диаметра такой окружности, можно получить так называемую сетку Воронова (Рис...).

На сетку Воронова очень похож рисунок чешуи ананаса...

Однако форма семечек не позволяет построить сетку Воронова по той причине, что абстрактно, каждая семечка является не точкой а неким отрезком, повернутым своей осью к центру подсолнуха. Поэтому, для моделирования формы семечек требуется иной алгоритм. Условно можно построить следующую геметрическую модель, которая еще нуждается в поиске точного алгоритма построения, похожего на алгоритм построения сетки Воронова (рис...)..

Найденный алгоритм моделирования спиральных структур в виде ветвлений позволяет получить инструмент для изучения целочисленных рядов. Так, например, «золотые» спирали с углами дивергенции в 137,51,   99,51 м 77,95  градусов дают количество ветвлений, соответствующее «золотым» аддитивным рядам

1-2-3-5-8-13-21-34-55-89...

1-3-4-7-11-18-29-47-76...

1-4-5-9-14-23-37-60-97...

Большой интерес представляют следующие за «золотыми» спиралями спирали основанные на пропорции корня квадратного из двух. Так, при угле дивергенции в 149,12,  105,45 и 81,56 градусов, ветвление спирали дает следующие значения (рис...).

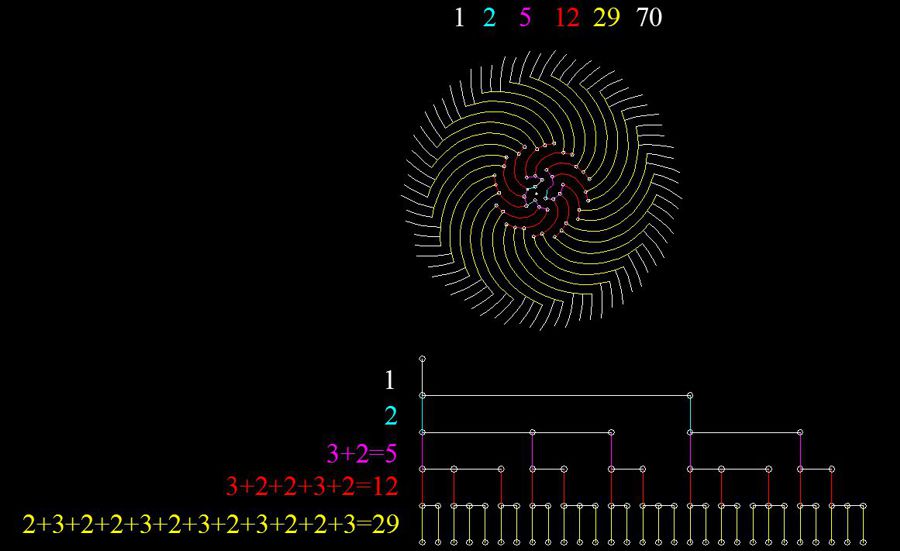
В данном случае также как и в предыдущем случае получаются аддитивные ряды, в которых каждый член ряда равен сумме двух предудущих к которым прибавлено еще одно значние предыдущего

1 - 2 - 5 - 12 - 29 - 70 - ... ;

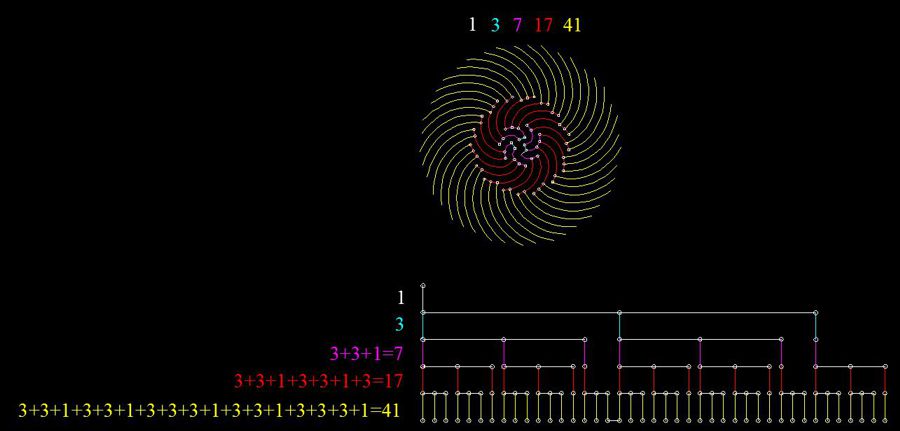
1 - 3 - 7 - 17 - 41- 99 - ...  ;

1 - 4 - 9 - 22 - 53 - 128 - ...

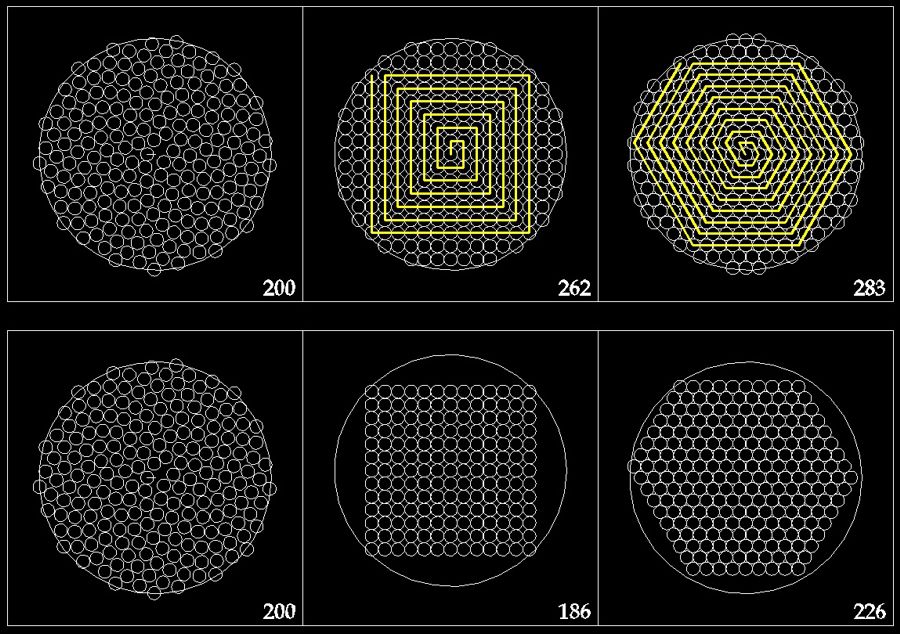
Оптимальность распределния узлов в круге имеет определенную специфику. Следует ограничиваться именно спиральными структурами. Плотность упаковки обычных тетрагональной или гексагональной структур является безусловно более высокой.

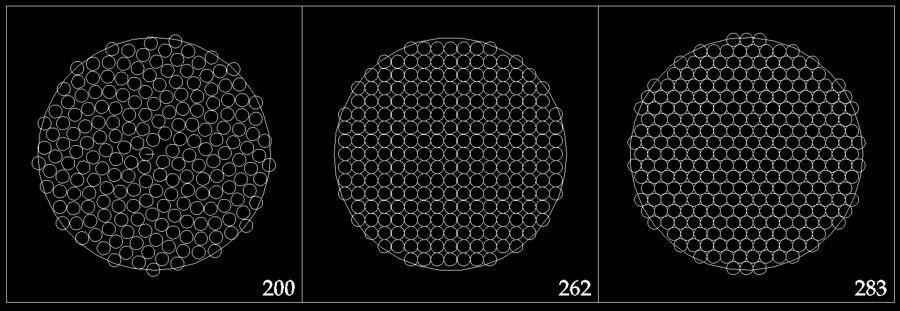
Разумеется, в тетрагональной и гексагональной структурах можно усмотреть некую спиральность, однако она будет стрмиться не к ругу, а к квадрату или шестиуголнику. 

В заключении попытаемся прояснить вопрос о месте золотого сечения в искусстве и архитектуре. Очевидно, что конструирование ряда природных организмов производилось с использованием "золотых" соотношений, которые позволяли оптимизировать некоторые параметры конструкции.

Попытаемся обозначить отличие архитектуры от проектирования. Архитектура может содержать игровой момент, допускающий следование неформализуемой художественной логике. А проектирование это жесткая однозначная определенность решения задач (конструкторских, планировочных и др.).

Поэтому золотая пропорция может иметь место в проектировании как элемент оптимизации какого-либо процесса или формы. Использование "золота" для "лучшения" художественной логики лишено смысла. Можно, конечно предполагать, что "золото" как-то резонирует с "аппаратом зрительного восприятия", но пока это только предположение. Можно попытаться "играть" с "золотом", но это будет игра с "игрушкой", но свободная игра "на рояле" осуществляется по неведомым и неформализуемым "законам" таинственной художественной логики.

"Живое произведение искусства отличается от мертвого тем, что в нем наряду с моментом "необходимости" есть момент "свободы". Живая линия отличается от линии проведенной по линейке, тем, что в каждой точкеона вольна пойти не так, а иначе, и вместе с тем обладает такой внутренней убедительностью, которая вынуждает нас признать, что мастер мог повести ее только так, а не иначе. Если бы этого не было, возможны были бы рецепты в искусстве, по одной части можно было бы механически размерить все прочие" (3).

Библиография:

1. Архитектурная бионка. Под ред. Лебедева Ю.С. М. Стройиздат 1990. 

2. Проблема филлотаксиса. Щетников А.И. Электронный ресурс.

3. Зубов В.П. Архитектурная теория Альберти. Дисс. на соиск. уч. ст. доктора искусствоведения. М. 1946.