Слово – не воробей,

а последовательность символов алфавита

«Золотое сечение и числа Фибоначчи – близнецы братья. Кто более матери истории ценен? – Мы говорим золотое сечение, подразумеваем числа Фибоначчи. Мы говорим числа Фибоначчи, подразумеваем золотое сечение».

Примерно так может начинаться гимн этим двум уникальным феноменам математики.

Их взаимосвязь несомненна. Она, что называется, заложена в них генетически.

Хотя принципиально, это две совершенно разные математические конструкции, объединенные между собой переходом от рекурсии или разностного (возвратного) уравнения к эквивалентному квадратному уравнению, и обратно:

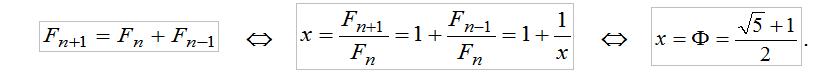
С использованием константы золотого сечения (ЗС) Ф можно сформировать степенной ряд 1, Ф, Ф², Ф³..., в котором каждый последующий элемент равно сумме двух предыдущих, а отношение между двумя соседними числами равно ЗС.

Аналогично число трибоначчи образует степенной ряд 1, Т, Т², Т³..., где каждое последующее число равно сумме трёх предыдущих, а отношение между двумя соседними числами равно константе Т – положительному корню кубического уравнения x³=x²+x+1.

Таким образом, прогрессия вида 1, Ф, Ф², Ф³... – геометрическая с одновременными свойствами арифметического ряда. Такое объединение двух признаков в одной модели часто называют аддитивно-мультипликативным свойством.

Добавляя к этим особенностям рекурсивный способ образования последовательности, можно говорить о «единстве аддитивных, мультипликативных и рекуррентных свойств эволюционных рядов Фибоначчи», как «прямом следствии диалектической триады» [1].

Исследуя золотое сечение, как правило, апеллируют, именно к числам Фибоначчи.

Заметим, что главенствуют здесь всё-таки не сами числа, а процедура их образования: двучленно-аддитивная рекурсия с единичными коэффициентами.

Ибо независимо от исходных (начальных) значений, своим предельным отношением соседних элементов последовательность всегда сходится к константе ЗС – аттрактору фибоначчиевой рекурсии, как максимальному по модулю корню адекватного характеристического уравнения.

Тем значительнее интерес к иным способам формирования числовых рядов, которые, так или иначе, связаны с золотым сечением. Например, в надежде найти новые интерпретации физического содержания этой удивительной фундаментальной константы.

Прочитать полный текст статьи в формате pdf