В настоящее время вопрос о мерах и пропорциях русских храмов 16-17 веков является крайне запутанным и противоречивым. С одной стороны это связано с крайне незначительным количеством исторических документов, освещающих эту тему. С другой стороны, почти полное отсутствие фактов привело к появлению множества гипотез, многие из которых можно причислять к разряду фантастических. Ситуация усугубляется еще и тем, что из-за тотальной недоверчивости и забюрократизированности чиновников найти какие-либо обмерные данные стало труднее, чем добыть секретные документы Генштаба министерства обороны. В отличии от нас, в странах Запада обмеры памятников давно уже все сделаны, систематизированы и опубликованы. Причем эта работа там началась еще в 16 веке, когда Андреа Палладио опубликовал результаты своих обмеров античных памятников. В России эта культура графической фиксации форм памятников архитектуры привилась только в во второй половине 19-го века. Однако героическими усилиями "строителей светлого и еще более светлого будущего" эта работа была сведена к предельному минимуму и сейчас в этой сфере архитектуроведения наблюдается почти полная разруха.

Поводом для написания данной статьи послужило любопытство, возникшее при наблюдении форм Георгиевской колокольни, находящейся на территории Коломенского музея-заповедника.

Ее форма является крайне необычной для всей русской архитектуры, так как в плане она построена на основе правильного пятиугольника. Если попытаться реконструировать логику построения такого плана, то первое предположение, которое приходит на ум, связано с пропорцией "золотого сечения". Это предположение имеет ряд косвенных оснований. В самом конце 15 века итальянским математиком Лукой Пачоли был написан трактат "О божественной пропорции" в котором он развил идеи древнегреческого математика Эвклида о способах построения правильных многоугольников. В трактате оформленном самим Леонардо да Винчи, приводятся чертежи и рисунки правильных многоугольников и многогранников среди которых важнейшее место занимает фигура правильного пятиугольника. Если допустить предположение что итальянские архитекторы того периода знали, почитали и использовали "золотую" пропорцию в своем творчестве, а также основываясь на фактах приезда итальянских зодчих на работу в Москву, можно также допустить мысль и о наличии "золота" в пропорциях колокольни. Кроме того, в последнее время появилось большое количество гипотез, которые объясняют все "секреты древнерусских зодчих" с помощью всяческих систем "золотых" саженей и пропорций. Однако, можно выстроить и другое предположение. Увязка итальянских влияний с "золотом" очень сомнительна, так как ни в одном трактате по архитектуре всех европейских авторов 15-18 веков о "золотой" пропорции нет абсолютно ни одного упоминания. Более того, если говорить о самом трактате Луки Пачоли, то обращает на себя внимание тот парадоксальный факт, что в добавленной главе об архитектуре и пропорциях человеческого тела о «божественной пропорции» нет никаких упоминаний. Поэтому рассмотрим другую версию. Деление круга на пять равных частей возможно осуществить по методу указанному еще у Витрувия, трактат которого активно переиздавался и комментировался в эпоху Возрождения. Витрувий, описывая годометр - устройство, которое измеряет длину пути приводит следующую формулировку - «пусть колеса повозки имеют четыре фута в поперечнике, так что если у колеса имеется отметка , от которой оно начинает вращаться вперед по поверхности дороги, то, повернувшись до той же отметки, с которой началось вращение, оно покроет определенное расстояние в двенадцать с половиной футов» (книга 10, глава 9).

Полученное в данном случае соотношение длины поверхности колеса к его поперечнику 25/8 служит Витрувию целочисленным заменителем числа «Пи». Следует отметить, что наряду с дробью 22/7, это соотношение с древних времен широко использовалось в математике и хозяйственной деятельности.

Используя гипотезу с соотношением 25/8, рассмотрим реальные размеры Георгиевской колокольни в плане. В вынужденно-неофициальном порядке мною был сделан один наружный замер колокольни с той стороны, где в том момент не было целого отряда бдительных милиционеров. Обмер производился лазерной рулеткой по прямому направлению от одной грани угловой пилястры до другой до другой.

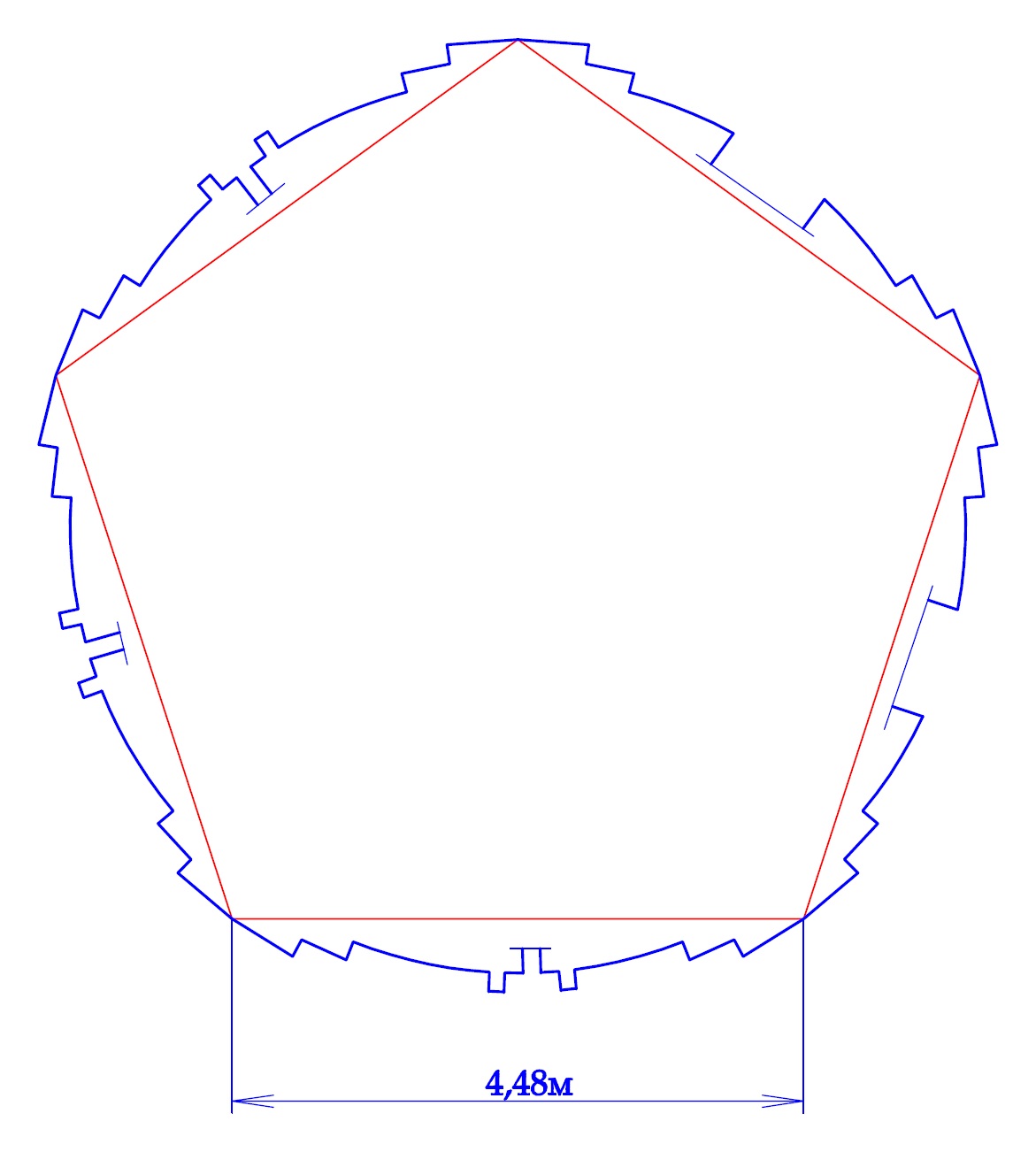
 Размер оказался равным 4,48м. Построим по этой грани правильный пятиугольник. В этом случае радиус описанной окружности получится равным 3,81м (диаметр - 7,62м). Если предположить, что зодчие Георгиевской колокольни использовали дробь 25/8, то получаем модуль равный 0,954м. В метрологическом отношении этот размер можно попытаться представить как величину, равную двум локтям по 0,477м. Размер такого локтя зафиксирован в «Цифирной счетной мудрости», относимой историками к концу XVI века. В ней отмечается, что в локте содержится 10 2/3 вершка и в трех локтях — два аршина или 32 вершка. Полагая величину аршина равной 0,71м, получаем величину в 0,473м, что кратно полученному в колокольне модулю.

Следует обратить особое внимание на то, что полученный модуль в среднем в три раза больше такого важнейшего конструктивно-технологического размера как длина кирпича (ложок) в сумме с одним швом кладки - 0,318м. Кроме того, эту величину, соотносящуюся с локтем в соотношении 2/3 по метрологическим данным следует интерпретировать как византийский фут, что по-русски обозначалось как стопа. Следовательно, в качестве рабочей гипотезы примем допущение, что длина кирпича (ложок) со швом в кирпичной кладке соразмерялась зодчими колокольни с размером византийского фута (стопы).

Переводя размеры плана колокольни в эти модули, получаем, что в длину окружности должно "уложиться" 75 ложков - футов. Разделив это количество на 5 частей, получаем, что одна сторона колокольни должна содержать в себе 15 ложков или 30 тычков. Детальное рассмотрение кладки стен колокольни косвенно подтверждает это предположение.

Разумеется, не приходится говорить о строго регулярной кладке стены, но в целом можно видеть, что в сумме на один «пролет» стены колокольни приходится 15 ложков или, полагая, что один «ложок» кладки соответствует двум «тычкам» - 30 тычков. 

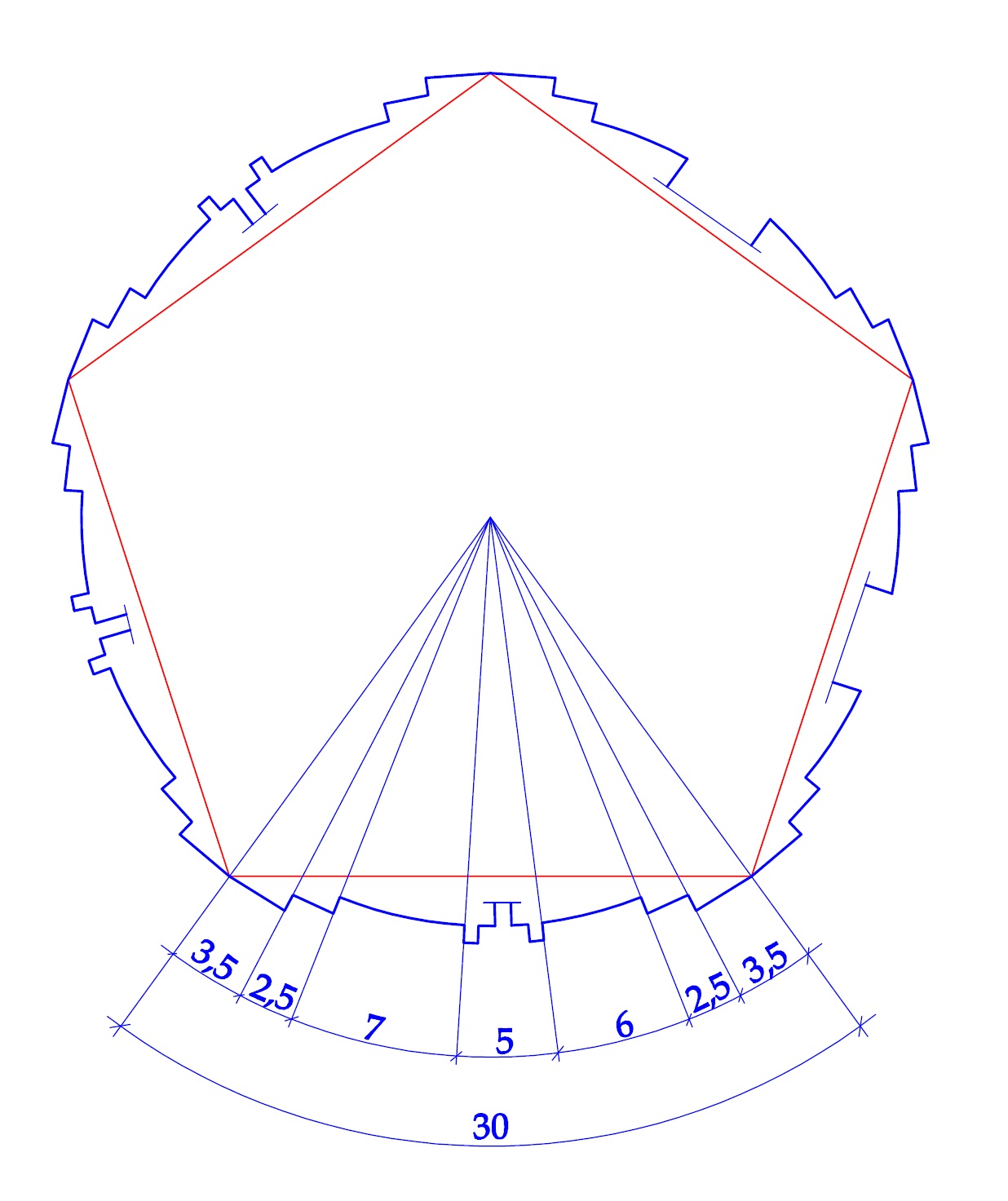
 Очевидно, что это предположение нуждается в дополнительной проверке. Невозможность получения других, более детальных источников информации по этому объекту, вынуждает нас опираться на такие весьма приблизительные данные.

План Георгиевской колокольни представляет интерес также в формально-теоретическом смысле. Так, в трактате Виченцо Скамоцци приводятся способы приближенного построения правильных многоугольников. Правильный пятиугольник «набирается» у него из десяти египетских треугольников 3х4х5.

В этом случае угол между большим катетом и гипотенузой получается равным 36,87 градусам, что приводит к суммарной погрешности в 8,7 градусов.

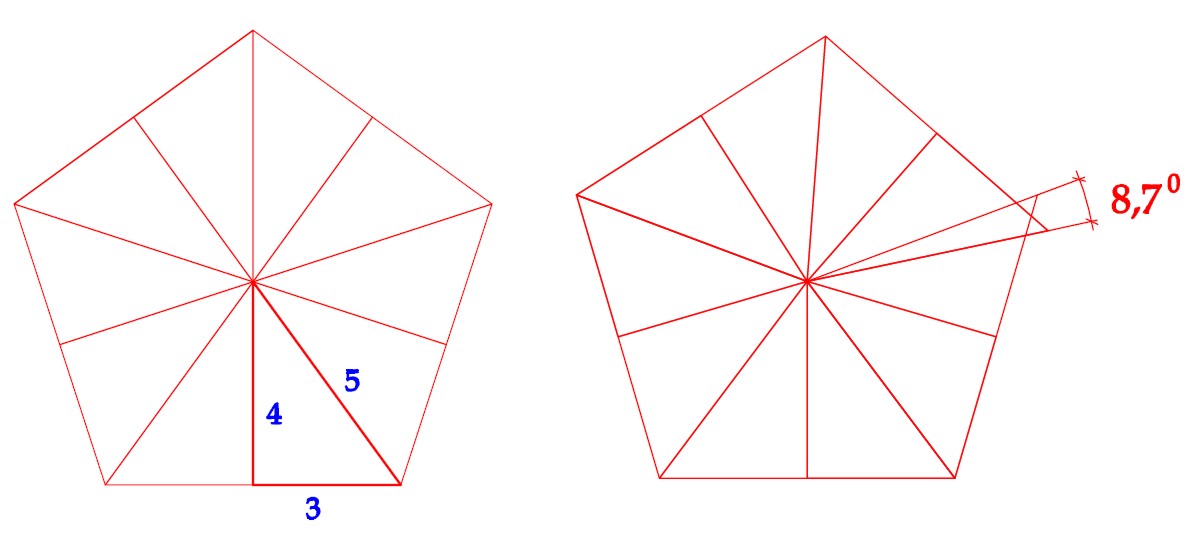
Если же попытаться реконструировать логику построения плана колокольни, то можно ее представить в виде следующей схемы с приближенно-целочисленными соотношениями. 

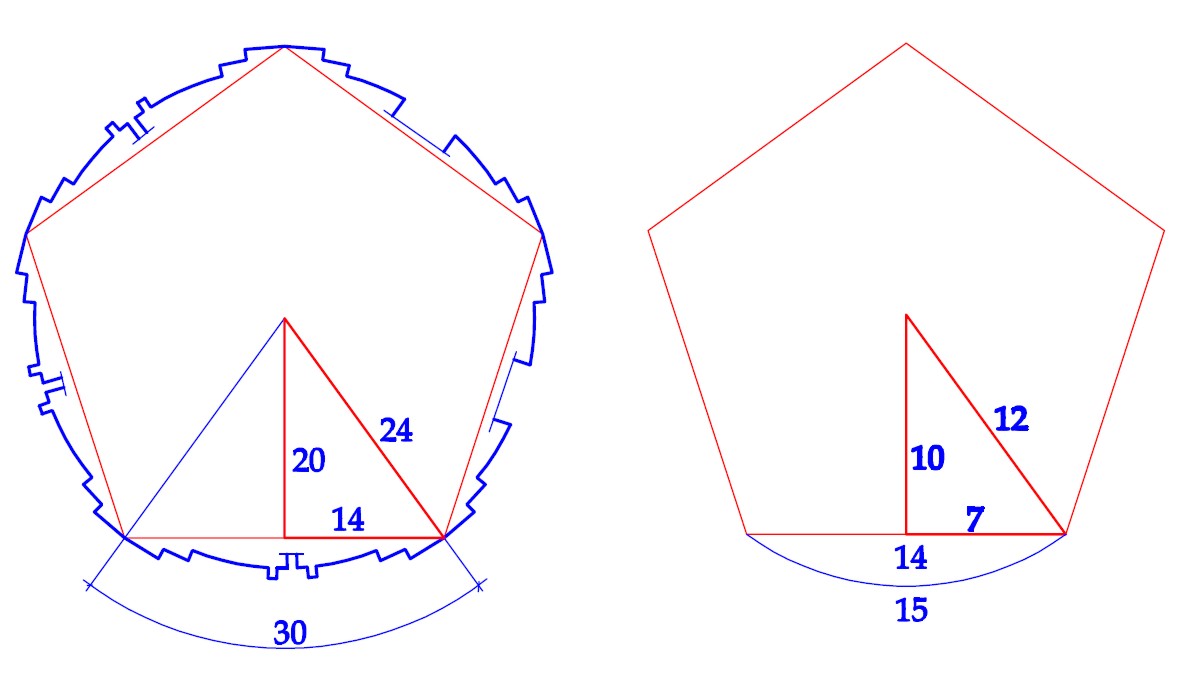
 Полученый в этом случае приближенно-целочисленный треугольник интересен тем, что соотношения 10/7 и 12/7 можно рассматривать как заменители таких иррациональных соотношений как корень квадратный из двух и корень квадратный из трех.

Такой треугольник является строго прямоугольным, но поскольку угол между болшим катетом и гипотенузой равен 35,26 градусам, то, в целом, набраный из таких треугольников пятиугольник будет иметь погрешность в 7,4 градусов. 

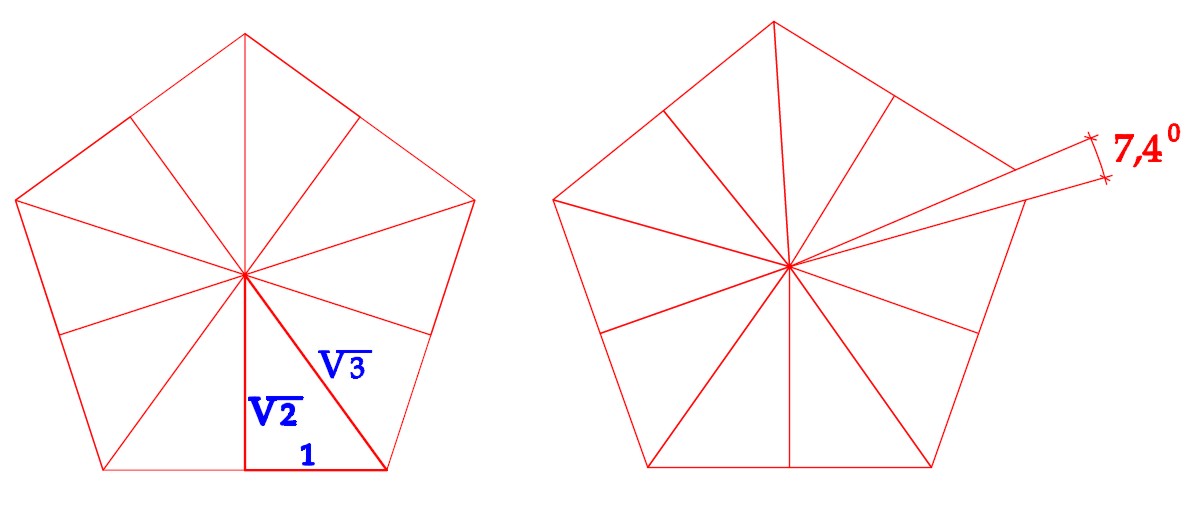
Если же вернуться к целочисленному треугольнику 7х10х12 и преобразовать его в равнобедренный треугольник 12х12х14, то складывая такой треугольник в пятиугольник получам погрешность равную всего 3,1 градуса. 

Учитывая, что модулем для построения данных треугольников служит размер длины кирпича, можно определить, что погрешность в 3,1 градусов на всю длину окружности, равной 75 ложкам или 150 тычкам, соответствует всего лишь 0,6 кирпича или примерно одному тычку. Для производства строительных работ такая точность приближения (1/150) приведенной гипотетической схемы представляется исключительно высокой. 

Очень характерно, что ширина башни оказалась фактически равной расчетному диаметру колокольни - 7,59м и 7,62м. Используя размер византийского локтя (0,477м) в качестве модуля, попытаемся сделать реконструкцию проектных размеров башни.

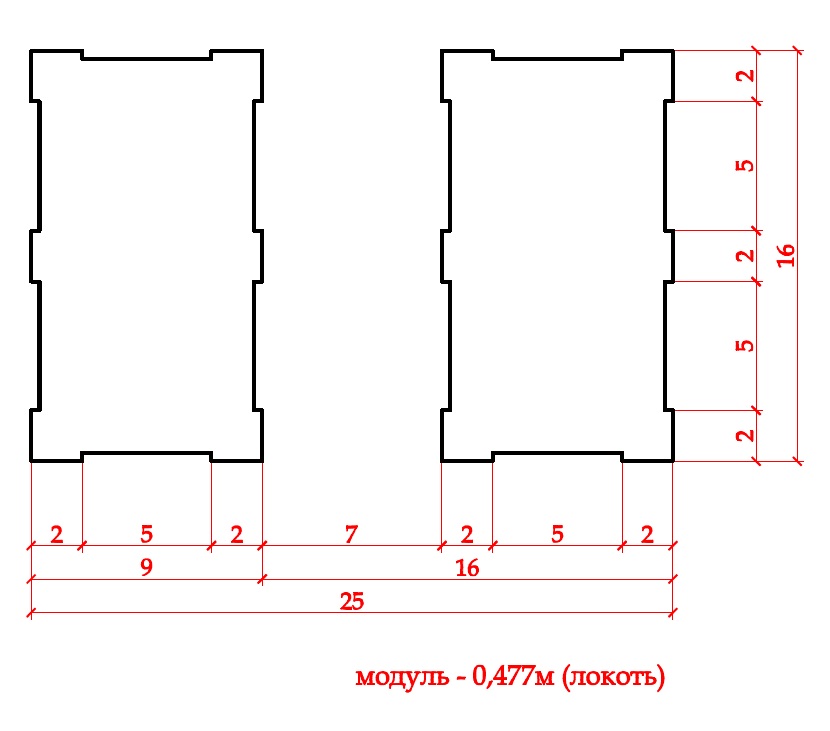
Разумеется, она соответствует фактическим обмерам с различными колебаниями. Так например, в водовзводной башне ширина угловых лопаток колеблется в пределах от 92 до 95 сантиметров, но в каждом случае они выложены шириной в три кирпича.  

Напрашивается вывод, что минимальным проектным  модулем для размерения плана водовзводной башни, так как и для Георгиевкой колокольни, следует считать размер тычка кирпичной кладки вместе со швом,  равный 1/2 византийского фута или 1/3 византийского локтя.

(продолжение следует)