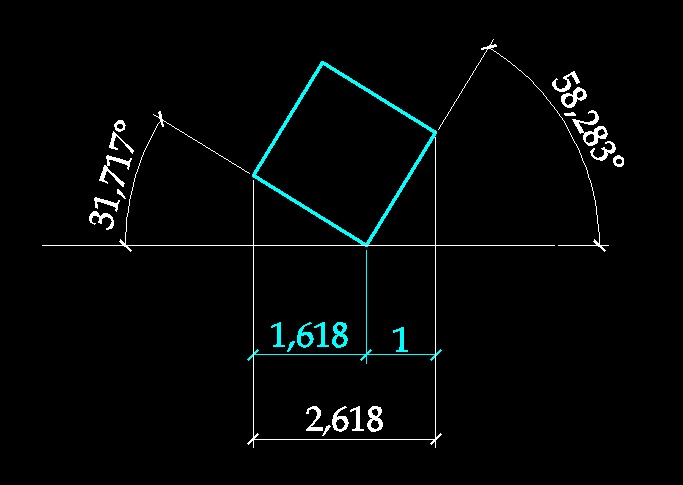
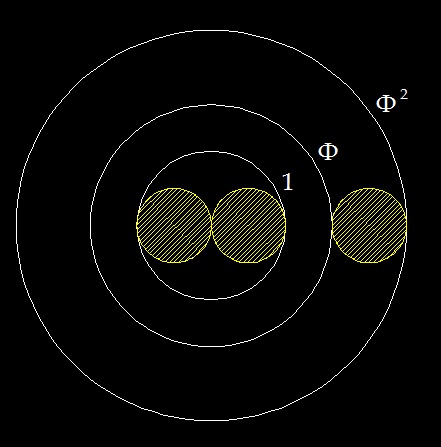
работе [1] была сделана попытка рассмотреть проблему филлотаксиса с помощью геометрического моделирования спиральных решеток. Поиски каких-либо оптимизирующих свойств пропорции золотого сечения тогда не увенчались успехом. Попытаемся посмотреть на геометрическую модель спиральных решеток с иной точки зрения. Попытаемся представить себе, что ромбовидная форма семечек в подсолнухе является производной от прямоугольника, имеющий некие, неопределенные пока, пропорции. Учитывая, что природа выбирает для спиральных структур числа Фибоначчи, можно «с ходу» предположить, что пропорция семечек также близка «золоту». Однако, натурные наблюдения показывают, что это не так. Так, в подсолнухе примерное соотношение между осями семечек, расположенным по разным направлениям, явно не равно «золотой» пропорции и, кроме того, не равно «квадрату» (рис.1).

 

 

Зададимся странным вопросом - какова пропорция такой ячейки. Для решения этой задачи попытаемся сделать геометрическое преобразование при котором криволинейная спиральная решетка превратится в прямоугольно-ортогональную решетку. Сделаем такое преобразование в произвольном рисунке (рис.2).

 

 

 

В конечной стадии получаем прямоугольный треугольник, катеты которого разбиты на части, соответствующие количеству спиралей. Гипотенуза такого треугольника представляет собой своеобразную зубчатую линию, которая соответствует краям корзинки подсолнуха (рис.3).

 

 

 

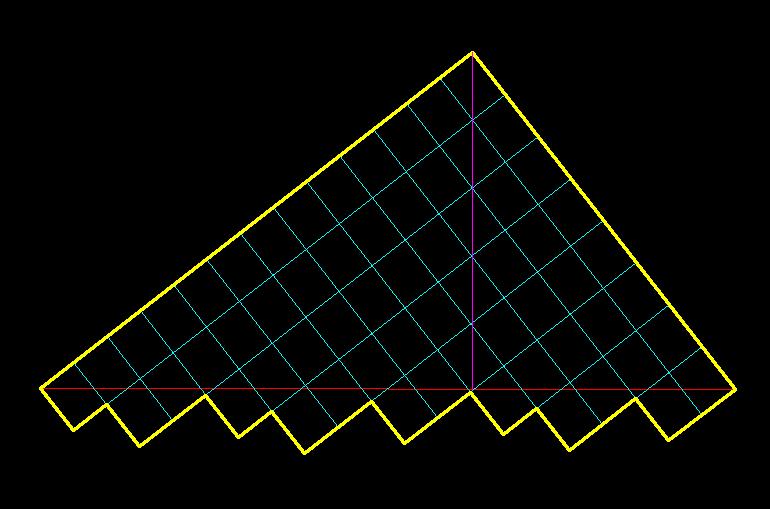
Любопытно, что расположение «зубчиков» не является случайным. «Зубчатая» линия набирается из «одинарных» и «двойных» «зубчиков» и их чередование соответствует структуре ветвления чисел Фибоначчи (рис.4).

 

 

 

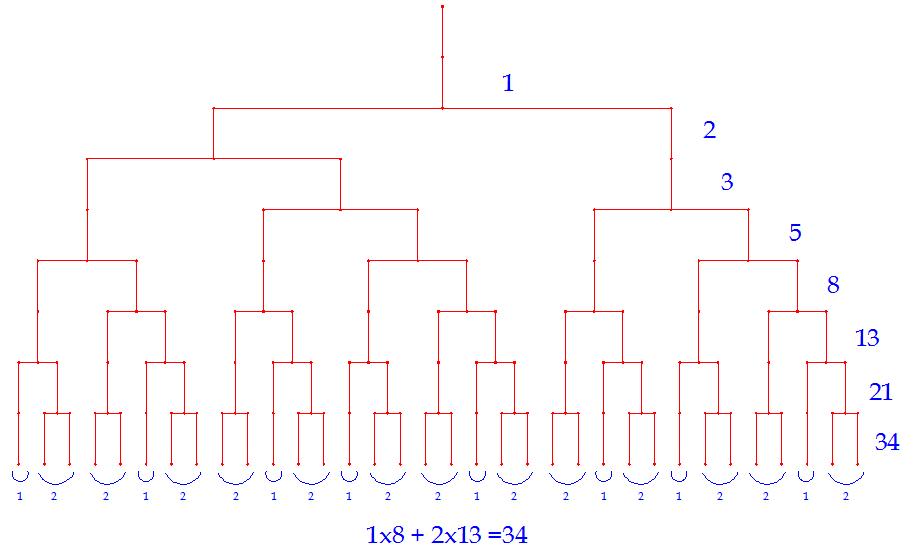
Сделаем предположение, что гипотенуза такого треугольника (преобразованный периметр окружности подсолнуха), состоящего из определенного количества одинаковых прямоугольников должна иметь минимальную длину. По нашим расчетам, если треугольник набирается из прямоугольников со сторонами А и В и, при этом один катет равен А х М а второй катет равен В х N, то минимальная гипотенуза получается в том случае, когда

А/В = sqrt (M/N)

Следовательно, при количестве спиралей 13 к 8, пропорция прямоугольной семечки-ячейки будет равна

А/В = sqrt (13/8) = 1,2747548

(рис.5)

 

 

 

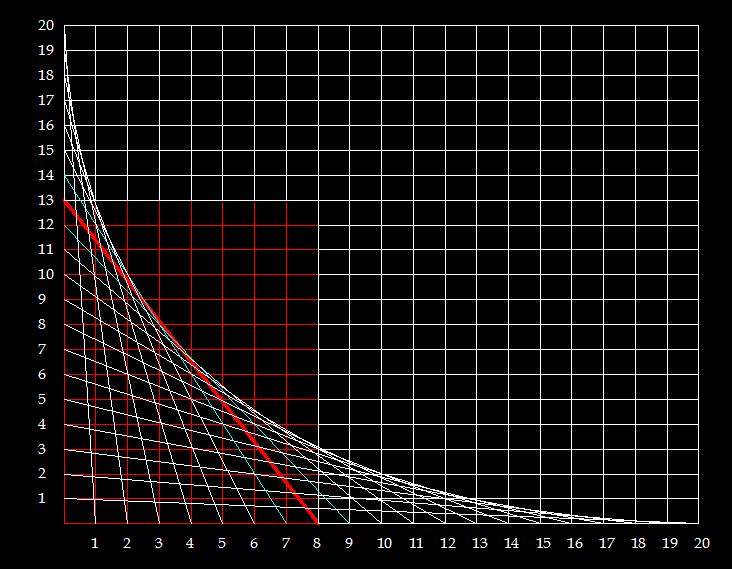
Для подсолнуха, который как правило имеет количество спиралей 55 к 34, пропорция семечки будет равна

А/В = sqrt (55/34) = 1,2718675

Очевидно, что в идеале, при увеличении количества спиралей соотношение M/N будет приближаться к «золотой» пропорции и, следовательно, в пределе, пропорция семечки будет равна sqrt (Ф).

При ином соотношении количества спиралей, пропорция прямоугольной ячейки будет иной. Так, например, при одинаковом количестве спиралей, допустим 14 на 14, пропорция ячейки при минимально возможной гипотенузе будет квадратной

А/В = sqrt (14/14) = 1

А если количество спиралей, допустим составляет 14 и 7, то пропорция ячейки будет равна

А/В = sqrt (14/7) = 1,4142135

Попытаемся определить, почему же все-таки природа выбрала именно такую пропорцию семечки-ячейки, приближающейся к значению sqrt (Ф)? По нашему предположению данный выбор был обусловлен необходимостью осуществления такого действия как возрастание количества спиралей филлотаксиса.
В работе [2] была подробно рассмотрена модель спирального филлотаксиса с квадратными зёрнами (рис.6).

 

 

 

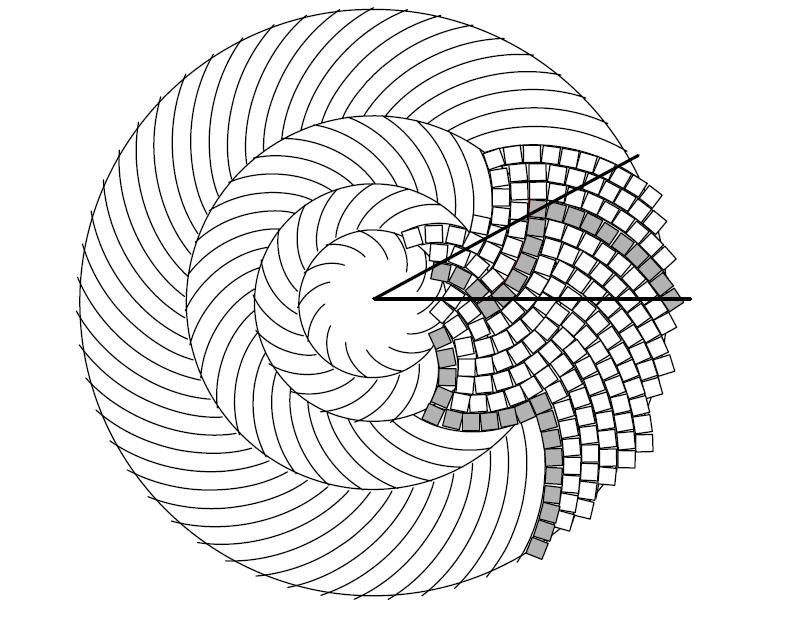
Если же попытаться построить подобную геометрическую модель но не с квадратными, а с ромбовидными зернами-семечками-ячейками то получится следующая картина (рис.7). 

 

 

 

 

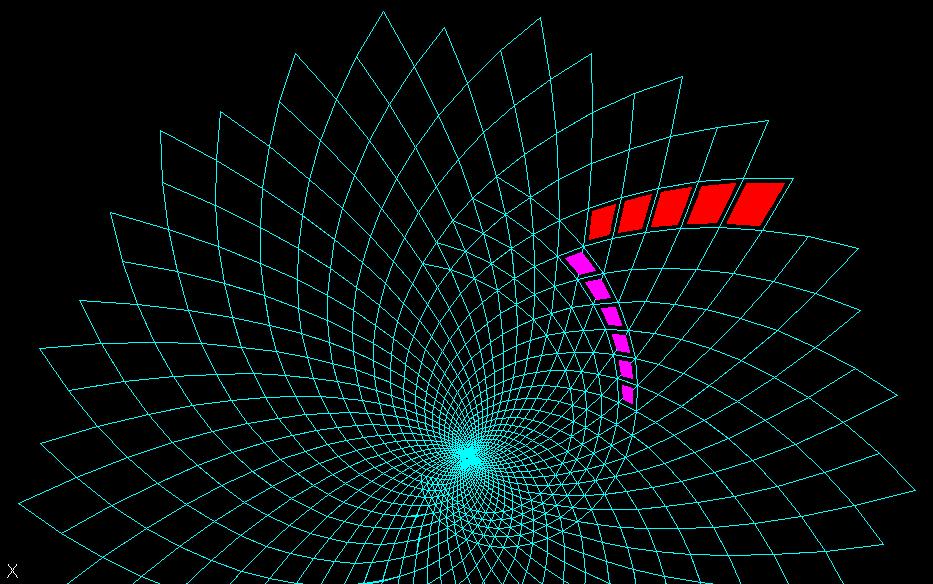
В этом случае видно, что спиральная решетка с количеством спиралей 34 на 21, преломляется и преобразуется в спиральную решетку с количеством спиралей 55 на 34 (рис.8).

 

 

 

 

 

 

 

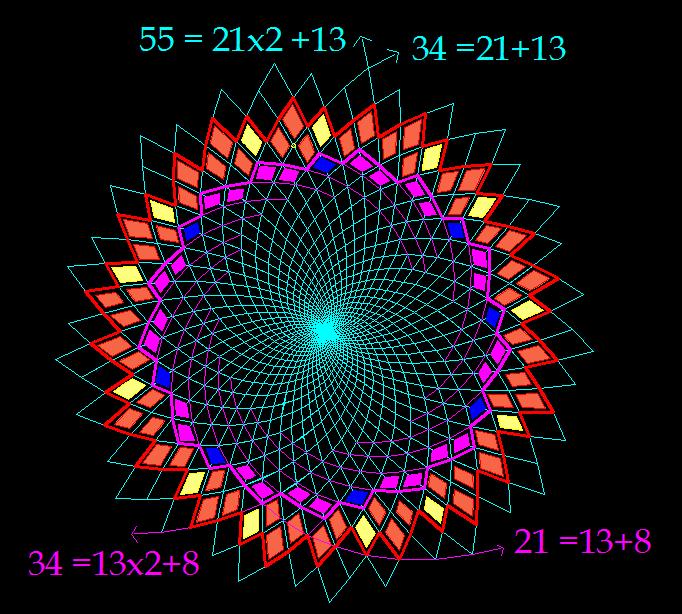
При этом, что самое важное, сами ячейки сохраняют геометрическое подобие (рис.9).

 

 

 

 

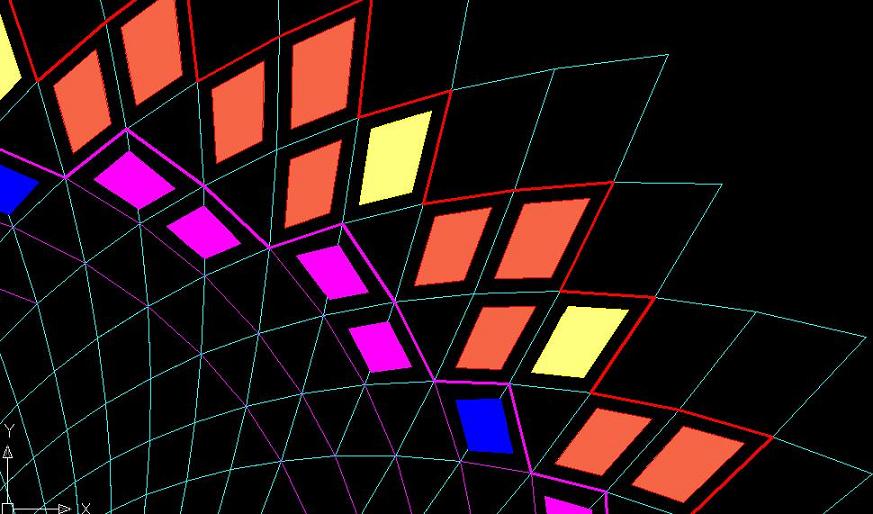
Если условно преобразовать ячейки в прямоугольники, то получится следующая схема возрастания филлотаксиса (рис.10).

 

 

 

 

 

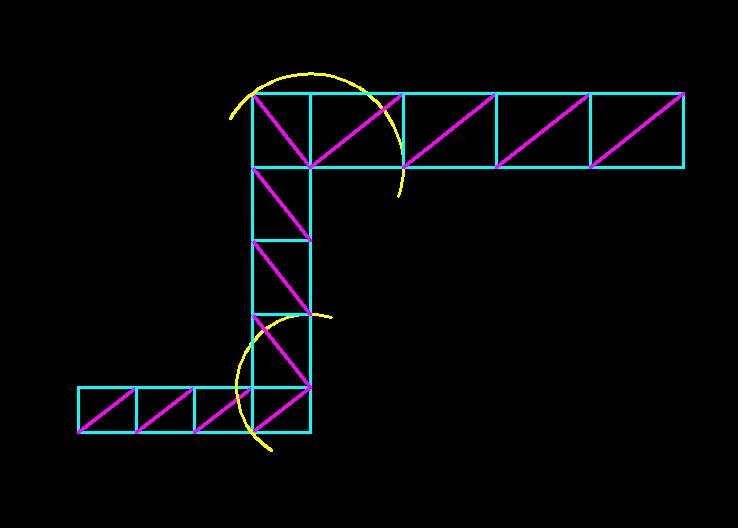
Важно отметить, каждая последующая ячейка подобна предыдущей и стороны каждой последующей ячейки состоят из большего катета и диагонали предыдущей ячейки. Следовательно, определим геометрическую особенность ячейки - диагональ ячейки так относится к ее большей стороне, как большая сторона относится к меньшей. Можно сформулировать и иначе - гипотенуза прямоугольного треугольника так относится к большему катету также как больший катет относится к меньшему катету. Решая, хорошо известную каждому искателю «золота», систему из двух уравнений, получаем следующее решение (рис.11).

 

 

 

 

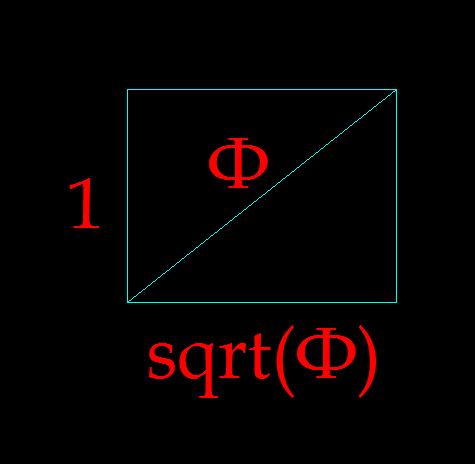
У данной задачи есть только одно решение и, следовательно, природные спиральные структуры могут релизовывать механизм возрастания филлотаксиса только при данной пропорции исходной ячейки - sqrt (Ф). По всей видимости, именно это является причиной появления "золотых" соотношений в спиральных природных объектах.

 

 

 

Дополнение от 20.01.13

Очевидно, что построение спиральных решеток с помощью логарифмичееских спиралей не совсем адекватно отражает реальную решетку в подсолнухах. Более целесообразно строить решетки с использованием спирали Архимеда. В этом случае картину возрастания филлотаксиса можно представить следующим образом (Рис.12).

 

 

 

 

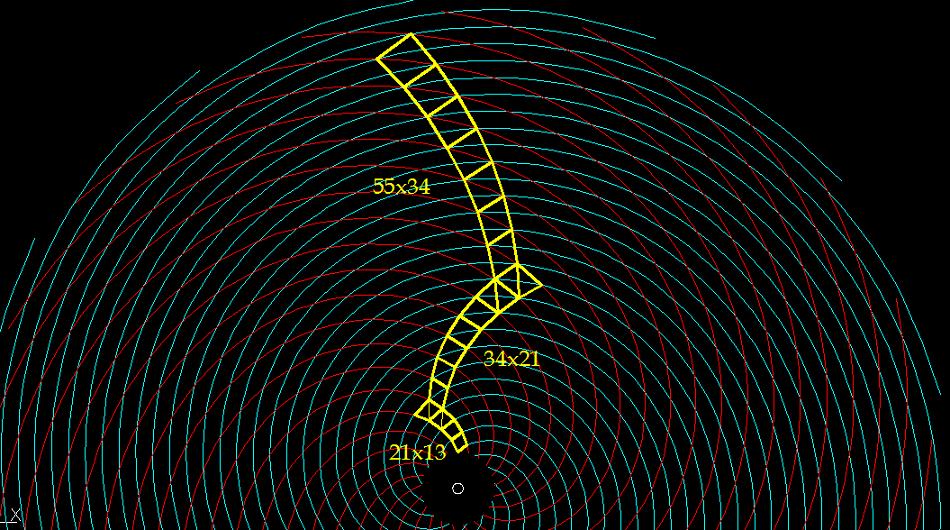
По всей видимости, полная картина бесконечно возрастающего филлотаксиса может быть построена на базе всего лишь трех спиралей, дающих соотношение из первых чисел Фиббоначчи - 2 к 1.

 

 

Дополнение от 22.01.13

Спираль Архимеда тоже не совсем точно соответствует реальному рисунку спиральных решеток в подсолнухе. По всей видимости, нужно использовать некую кривую, которая "выходит" из малой (внутренней) окружности под прямым углом (ортогонально) и "примыкает" к большой (внешней) окружности по касательной (Рис.13)

 

 

 

 

 

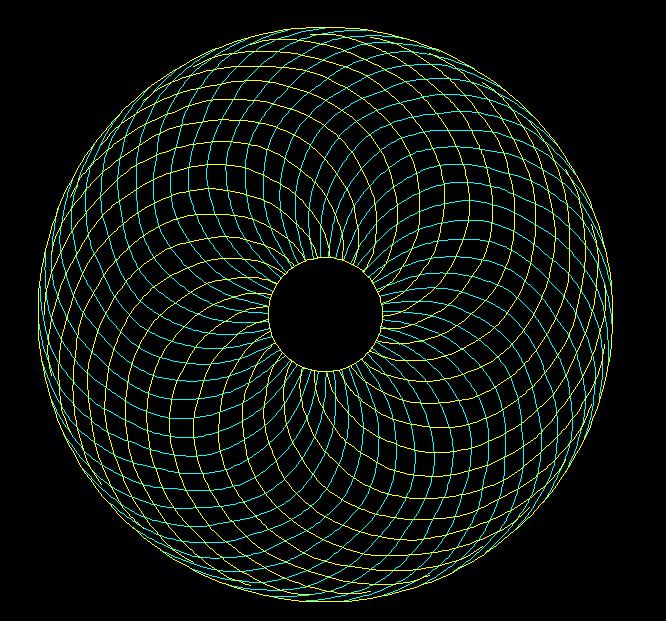
Дополнение от 23.01.13

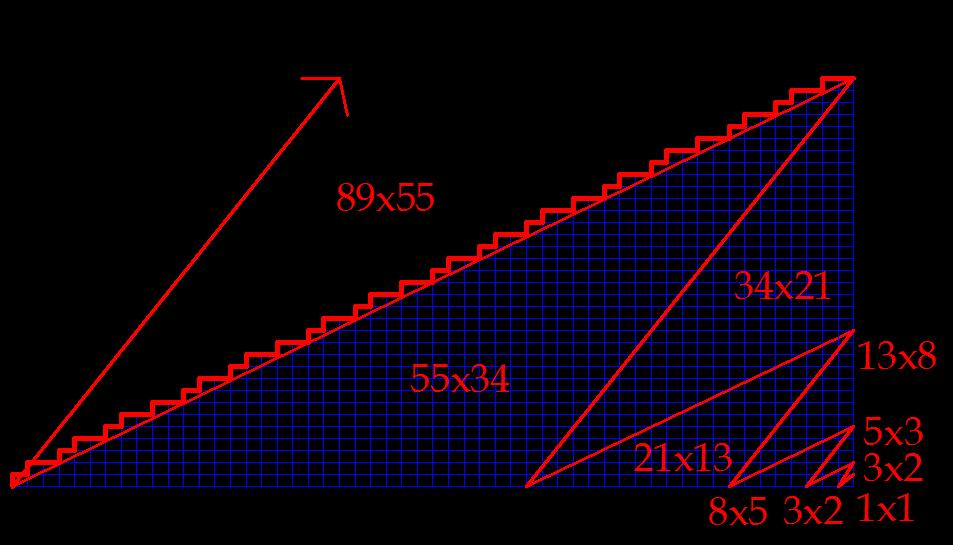
Исходя из схемы спиральных решеток 55х34 (Рис.14)

 

 

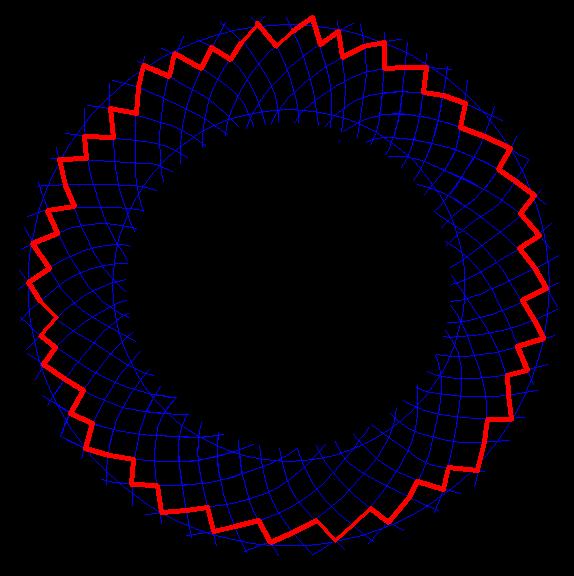
выстроим схему бесконечно возрастающего филлотаксиса (Рис.15).

 

 

 

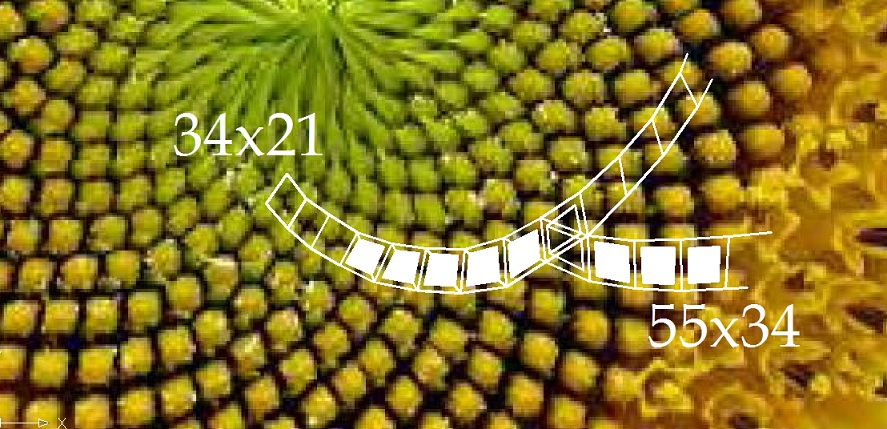
Дополнение от27.01.13.

Еще один "фантик". На рисунке 16 показана схема перестройки одной спирали (34х21) в другую (55х34), при этом "диагональ" ячейки одной спиральной решетки преобразуется в "сторону" ячейки другой спиральной решетки.

 

 

 

 

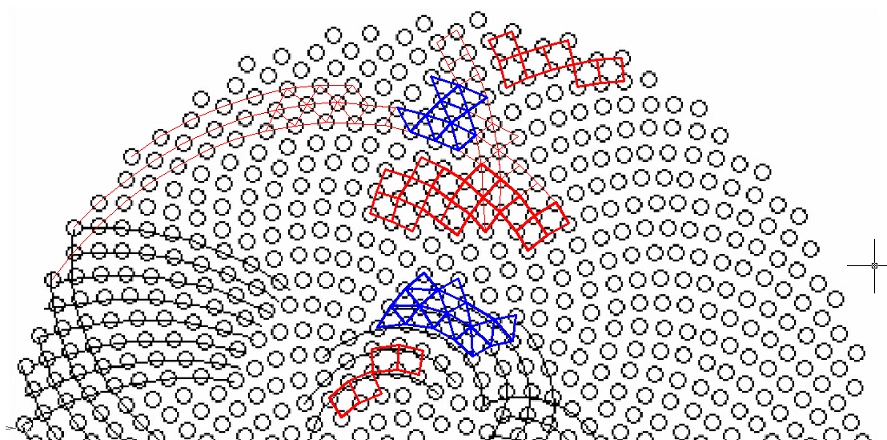
Дополнение от 03.02.13

И еще один "фантик". Если основываться на "шариковой" модели укладки ячеек в корзинке подсолнуха то, полагая, что все шарики одинаковы, можно заметить, что происходит постоянная перестройка в кольцевых зонах. Тетрагональная укладка шариков постепенно меняется на гексагональную и наоборот. Данная особенность отлично согласуется с теорией филлотаксиса А.Г.Малыгина. Очевидно, что "укладка""зубчиков" в кольцах будет соответствовать структуре ветвления чисел ряда Фибоначчи (или ряда Люка) в соответствии с рис.4 данной статьи. Вот такая вот растущая кристаллизация получается...

 

 

 

 

 

 

 

 

 

 

 

 

 

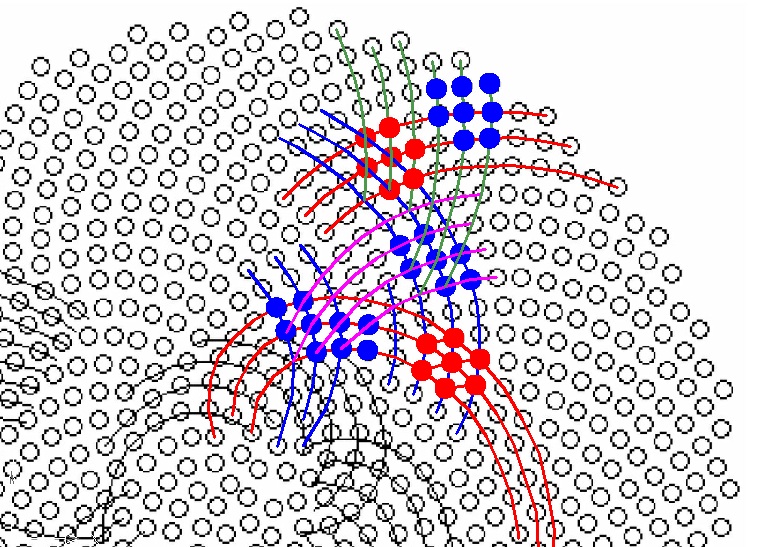
Дополнение от 05.02.13.

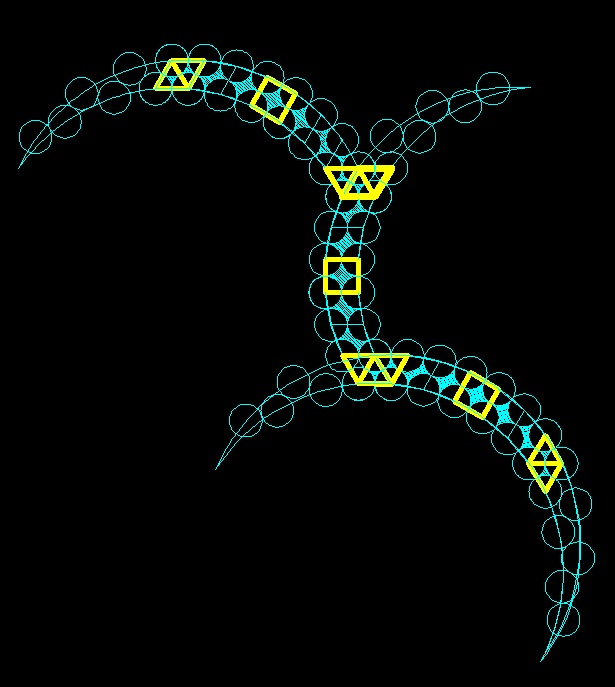
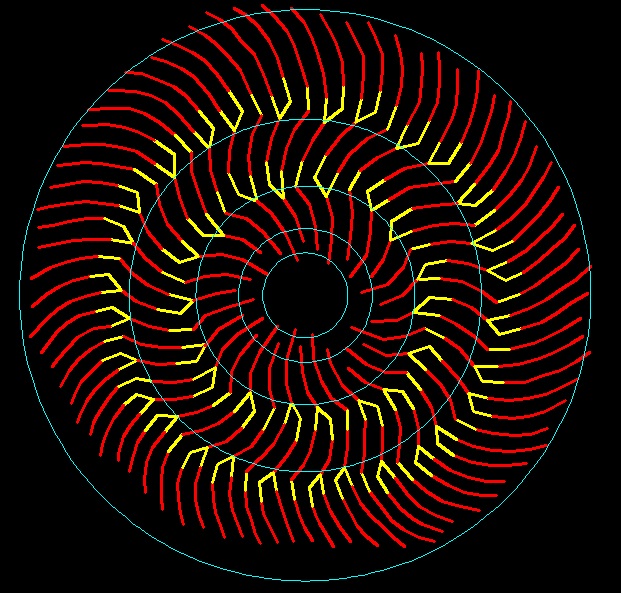
Еще "фантик". Логику ветвления спиралей в подсолнухе можно смоделировать следующим образом - зона с приближенно гексагональной укладкой ячеек (желтый цвет) дает возможность произвести перестройку с  увеличением количества спиралей. На рисунках видно как малое количество приближенно тетрагонально упакованных спиралей (белый цвет) к переходит большему количеству (голубой и песочный цвет) спиралей.

 

 

 

 

 

 

 

 

 

 

 

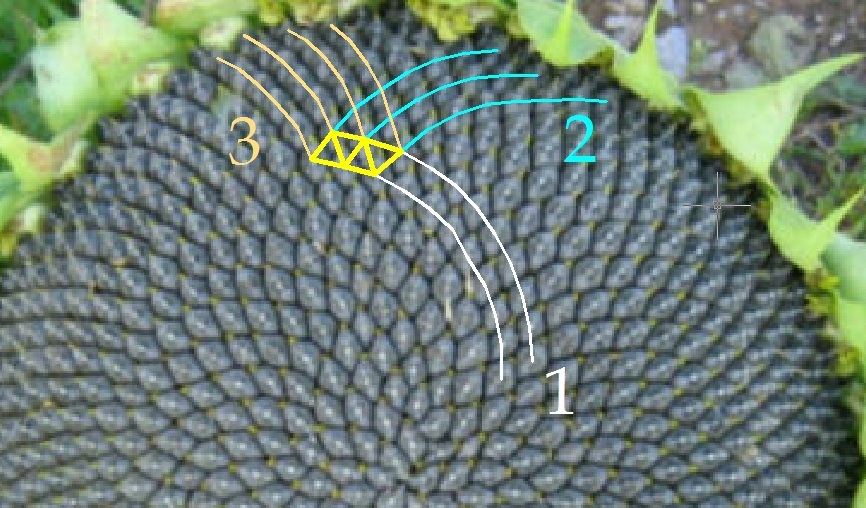
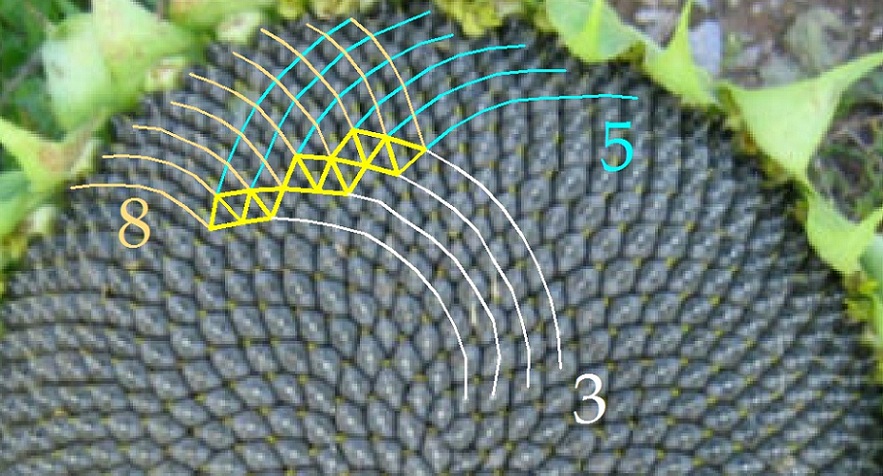
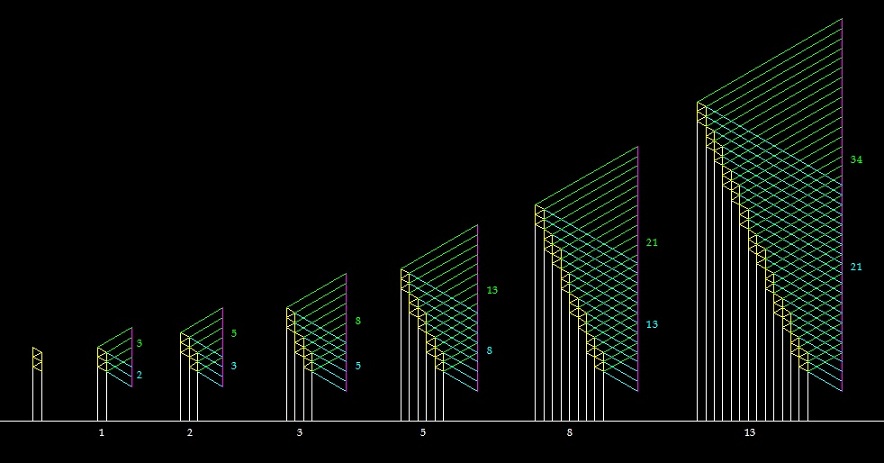
Дополнение от 08.02.13

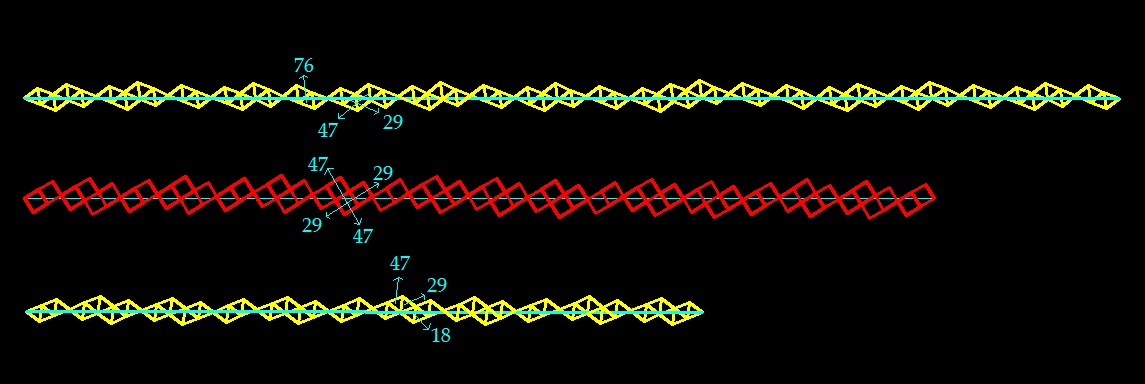
Ветвление спиралей в подсолнухе аналогично обычной структуре ветвленияч чисел ряда Фибоначчи (или ряда Люка).

 

 

 

 

 

 

 

Длины окружностей и их радиусы соотносятся в "золоте"

 

 

Дополнение от 10.02.13

Модель подсолнуха представляет собой сложный набор спиральных решеток из которых составляются чередующиеся колецевые зоны с приближенно-тетрагональными и приближенно-гексагональными структурами. В приближенно-тетрагональных зонах решетка «набирается» из N правых и М левых спиралей (допустим, что М больше N). При переходе через приближенно-гексагональную зону происходит перестройка спиральной решетки - М левых спиралей переходят в следующую приближенно-тетрагональную зону без изменений, а количество правых спиралей представляет собой сумму M+N. Отсюда следует, что количество спиралей возрастает аналогично аддитивным числовым рядам (каждый последующий член равен сумме двух предыдущих). Таких рядов бесконечно много. Однако, для сохранения подобия спиральных ячеек в тетрагональных зонах, должно соблюдать следующее условие

(M+N)/M = M/N

т.е. в таком аддитивном ряду каждый член ряда должен соотносится с младшим так, как старший соотносится с ним самим. А этому условию, как известно, приближенно соответствуют два аддитивных ряда - ряд Фибоначчи и ряд Люка. Использование именно этих рядов дает возможность природе осуществлять возрастание количества спиралей (возрастание филлотаксиса) с сохранением подобия спиральных ячеек. 

 

 

 

Дополнение от 12.02.13

 

Люди работают в данном направлении - http://journals.iucr.org/a/issues/2012/04/00/eo5015/eo5015fig12.html

 

http://arxiv.org/pdf/1201.1432v2.pdf

Добавление от 12.02.13

 

 

 

Дополнение от 16.02.13.

Появилась возможность строить заполение корзинки подсолнуха в автокаде:

 

 

 

Дополнения от19.02.13

Загружаю новые иллюстрации. Интерпретация будет позднее..

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

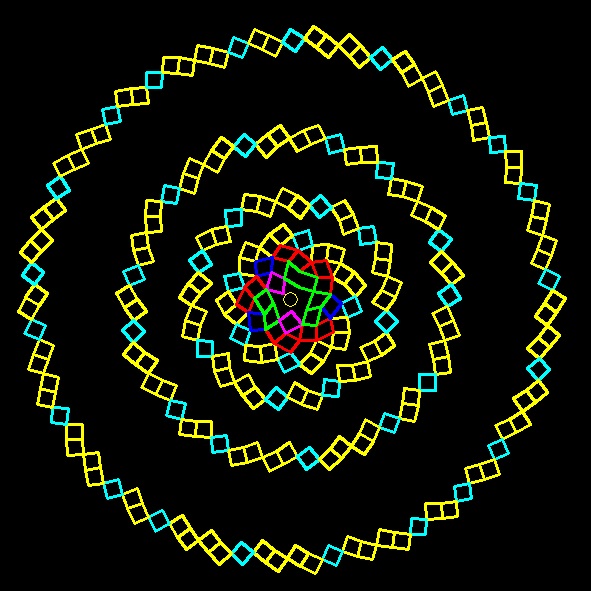
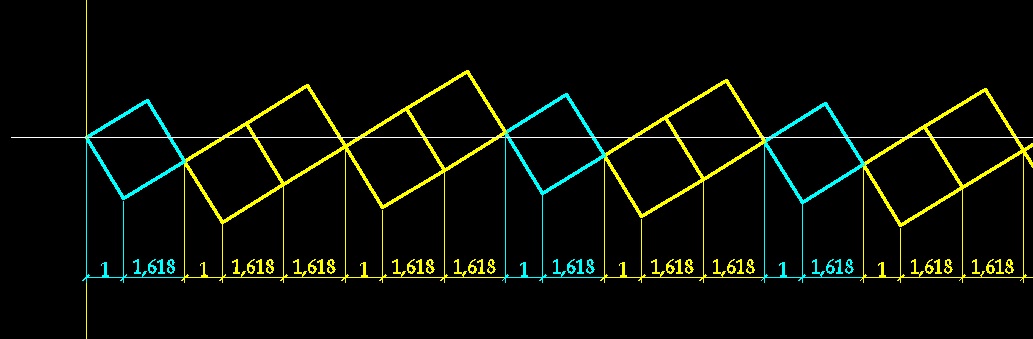
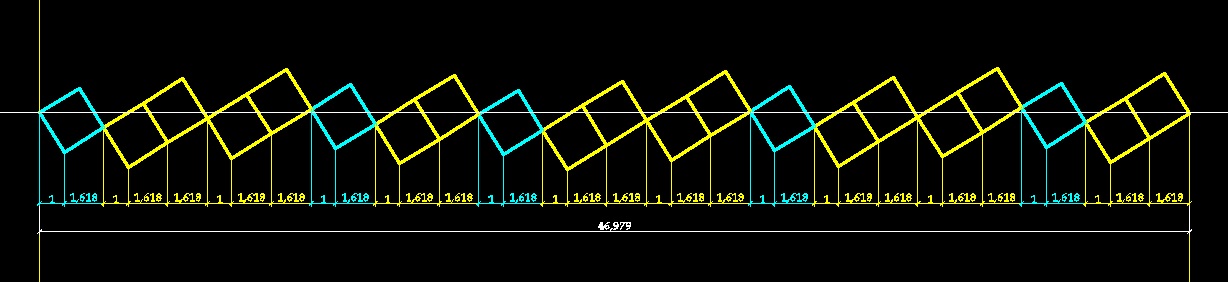
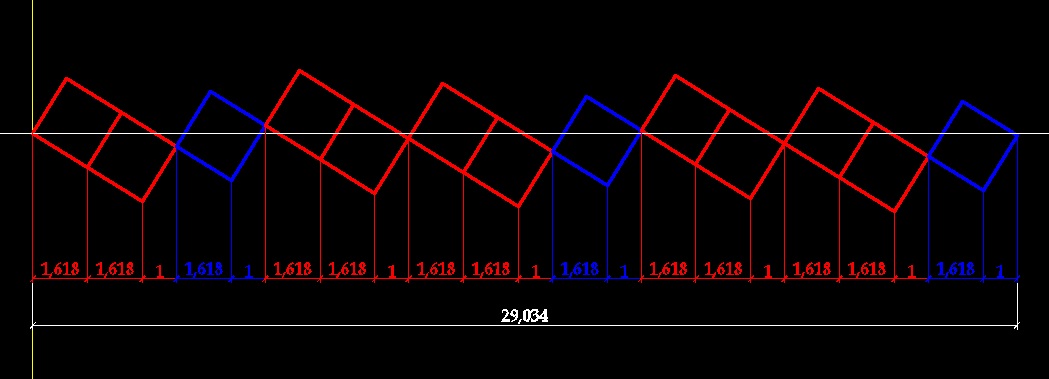
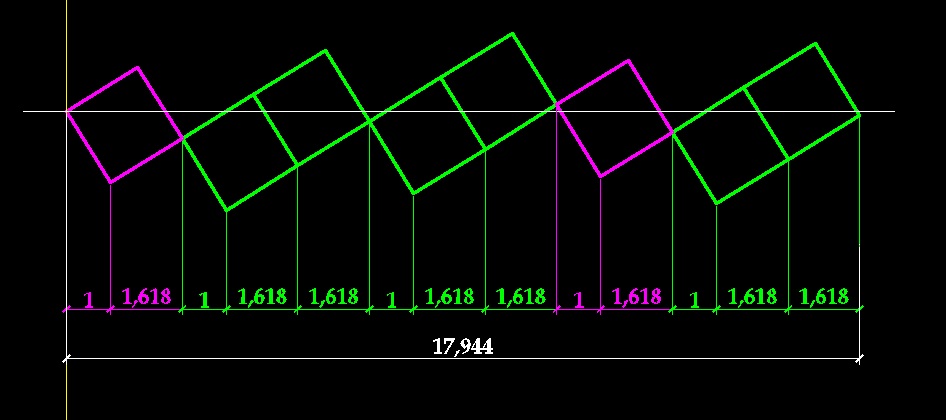
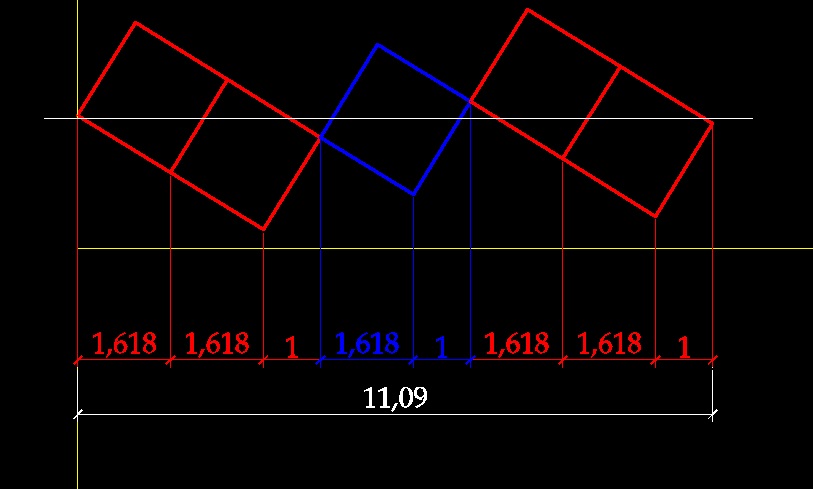
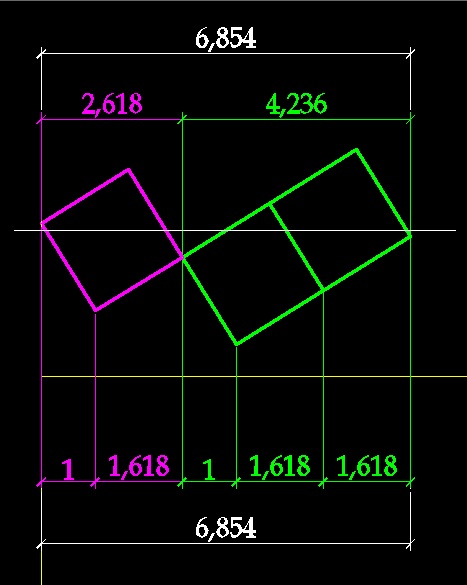
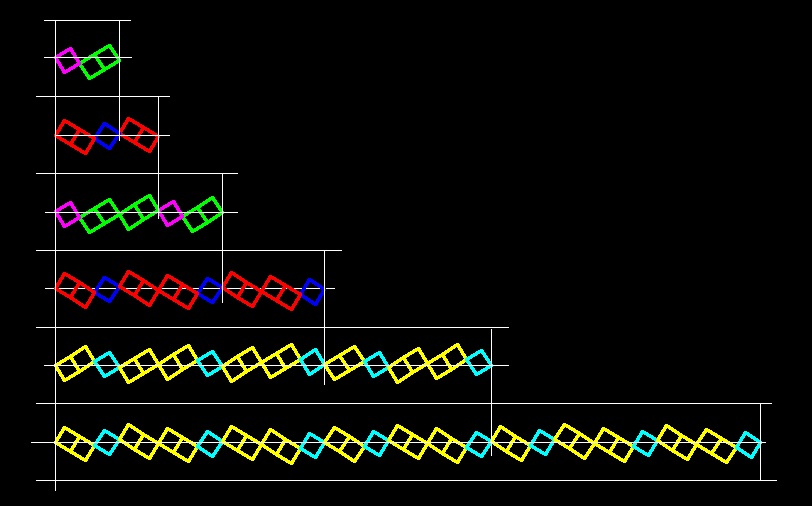
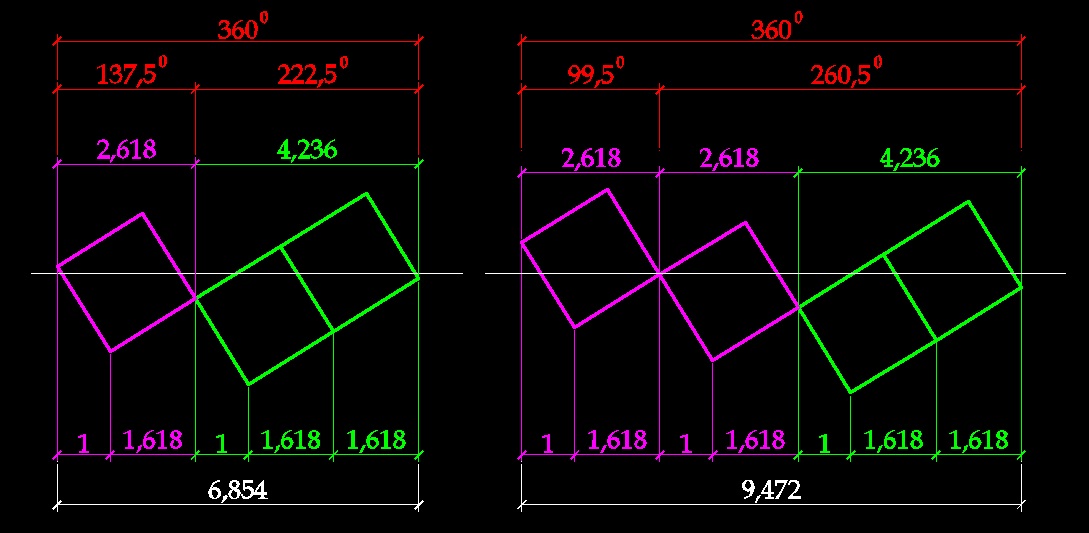
Вот отсюда получается угол дивергенции семян - 137,5 градусов. Если полный отрезок (выпрямленную длину окружности) разделить на меньшую часть (6,854/2,618) то получим 2,618.  Аналогично 360 градусов делим на 137,5 градусов, получаем 2,618

 

 

 

А вот так получается сбой при котором угол дивергенции становится равным 99,5 градусам и спирали в подсолнухе выстраиваются по ряду Люка.

 

 

 

 

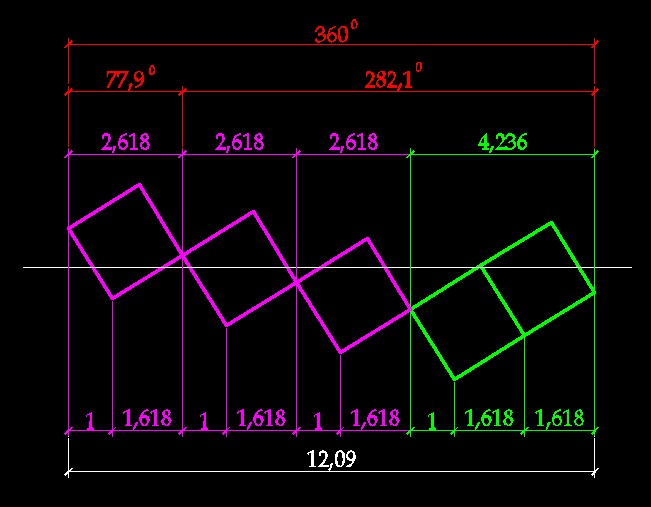
Дополнение от 21.02.13.

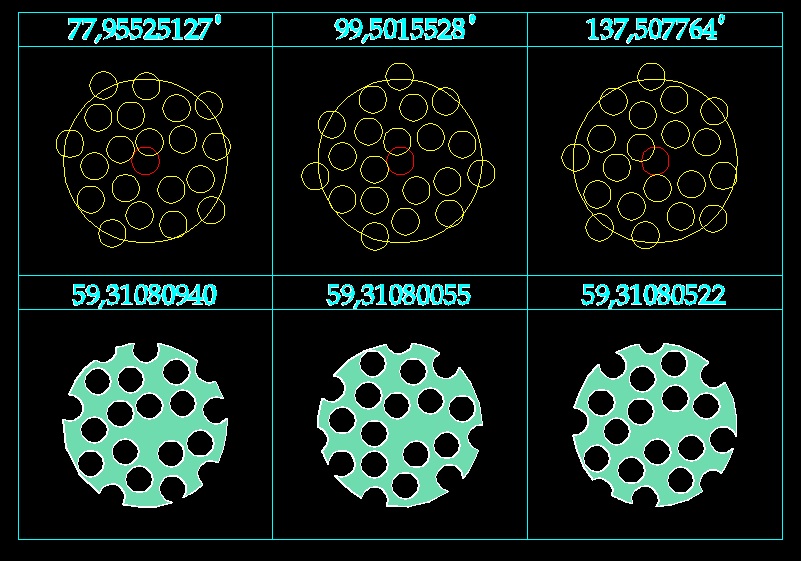
Нашел способ экспериментального выбора оптимального угла заполнения площади круга одинаковыми кружочками меньшего радиуса. Минимальная площадь пустот между кружочками рассматривается как критерий оптимального заполнения.

Малое значение площади при угле дивергенции в 100 градусов говорит о его близости углу в 99,5 градуса. А минимальная площадь как и ожидалось получается при угле конвергенции в 137,5 градусов.

Любопытно, что точный угол в 99,5015528 градуса дает чуть-чуть меньшую площадь пустот, чем "правильный" угол в 137,507764 градуса. Следовательно получается, что он чуть-чуть оптимальнее по сравнению с другими "золотыми" углами.

 

 

 

Дополнение от 24.02.13

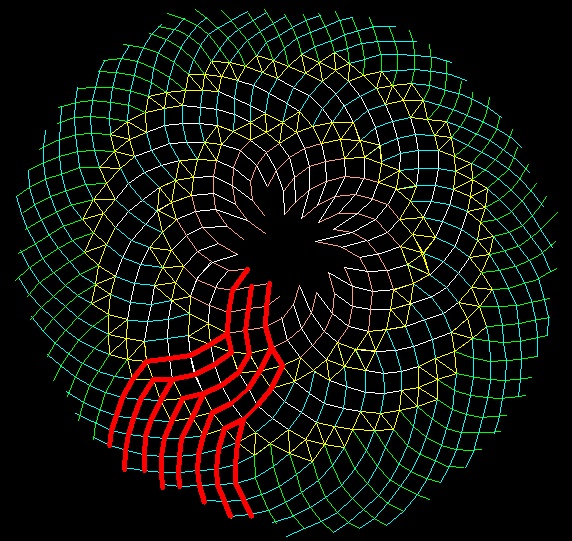
Полученная структура ветвления имеет такую визуально наблюдаемую особенность - ширина всех "коридоров" "лабиринта" постоянна (см.рис.)

 

С увеличением радиуса окружности "подсолнуха", происходит 2 процесса:

1. увеличение количества "коридоров" (в местах перегибов);

2. постепенный поворот оси коридора от "радиального" положения к "кольцевому".

 

 

Добавление от 24.02.13.

И все-таки угол дивергенции семян в 137,507763 градуса дает более плотную упаковку корзинки подсолнуха, чем угол 99,5015528 градусов. Разница микроскопическая, но она есть.

 

 

 

 

Дополнение от 03.03.3

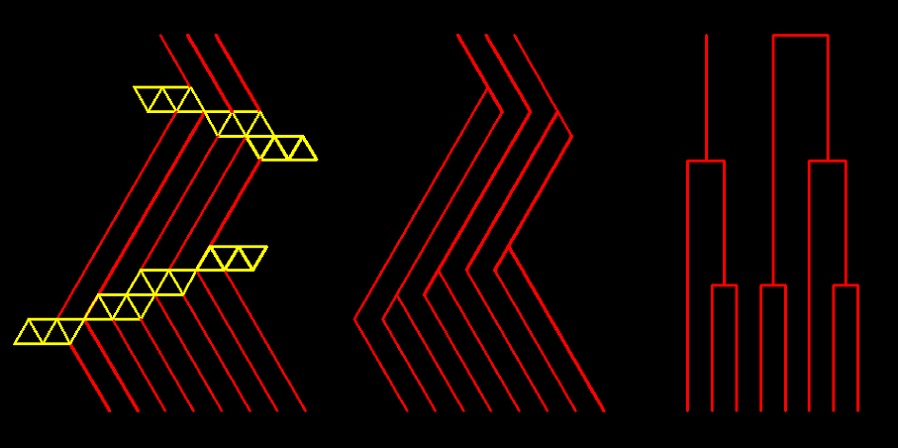
К вопросу о логике построения спиралей подсолнуха.

 

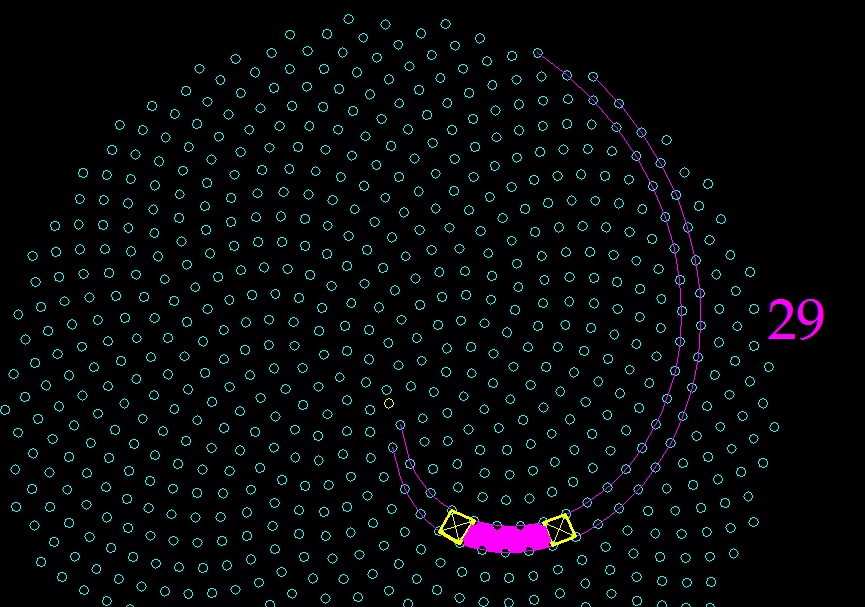
Природа использует только самый "широкий" участок между двумя соседними спиралями Ферма.

 

 

 

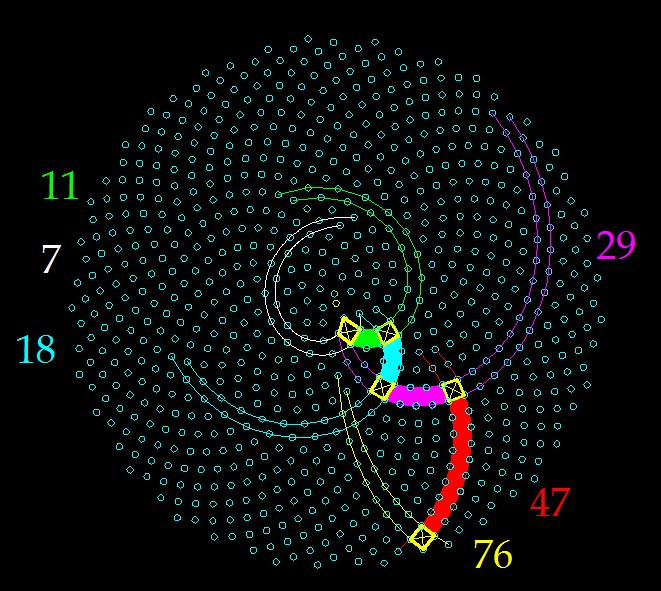
Дополнение от 08.03.13

Аналогия между линейными и круговыми величинами...

 

 

 

 

 

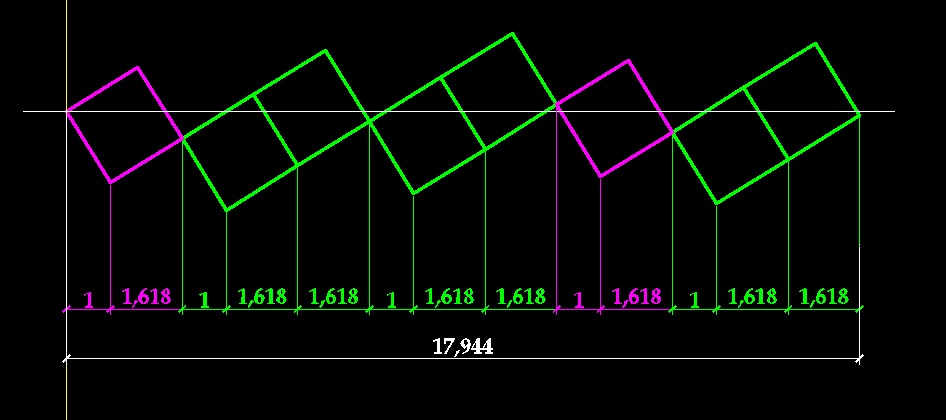
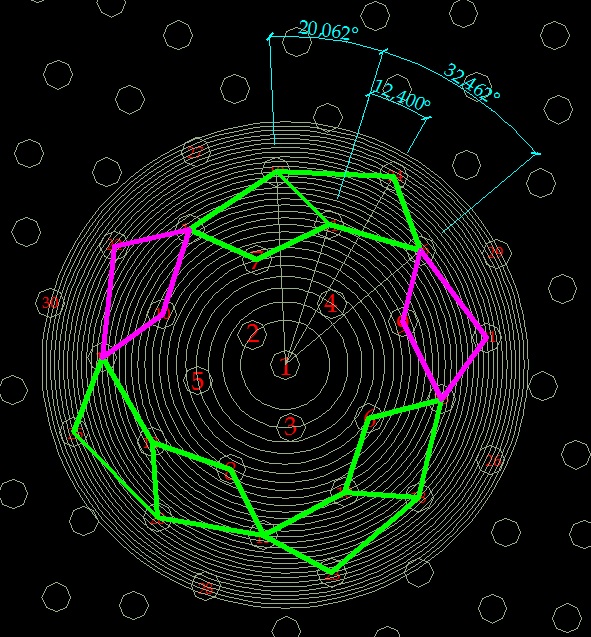
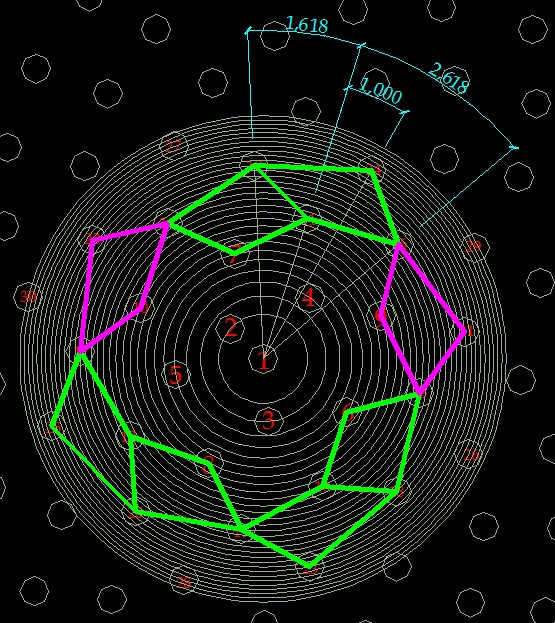
Дополнение от 09.03.13

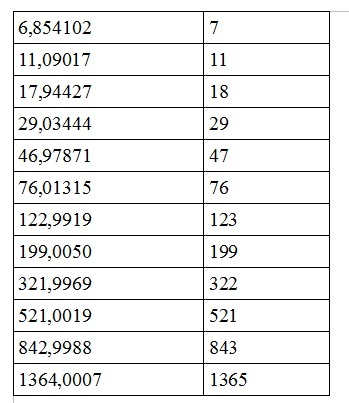
Поиск симметрии возрастающего филлотаксиса показал, что деление круга на 9 равных частей может дать весьма точную "раскладку" подобных элементов.

 

 

 

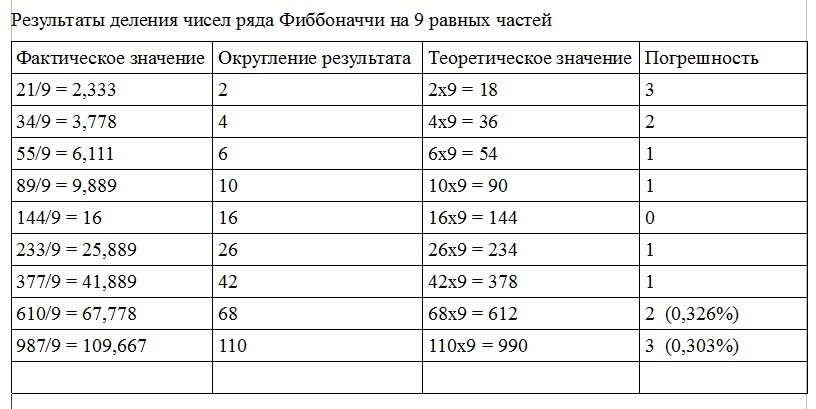
Девятка получается как результат деления золота в шестой степени на два (17,94427/2=8,97214). Второй столбец таблицы представляет собой ряд удвоенных чисел Фибоначчи.

 

Дополнение от 04.08.13

 

Опосредованно мы получаем задачу на заполнение круга группами тождественных фигур (четырехугольников).  Получается некая круговая симметрия...

 

 

 

 

 

 

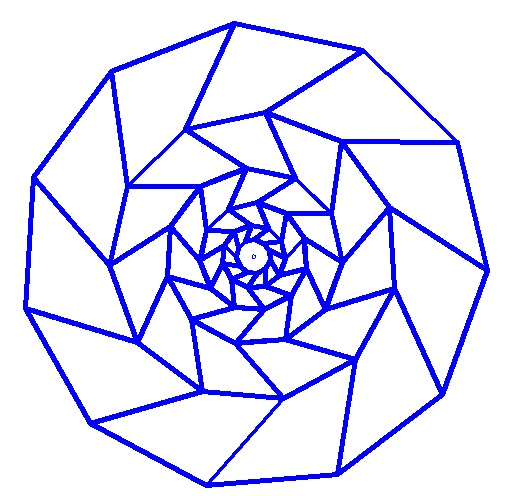
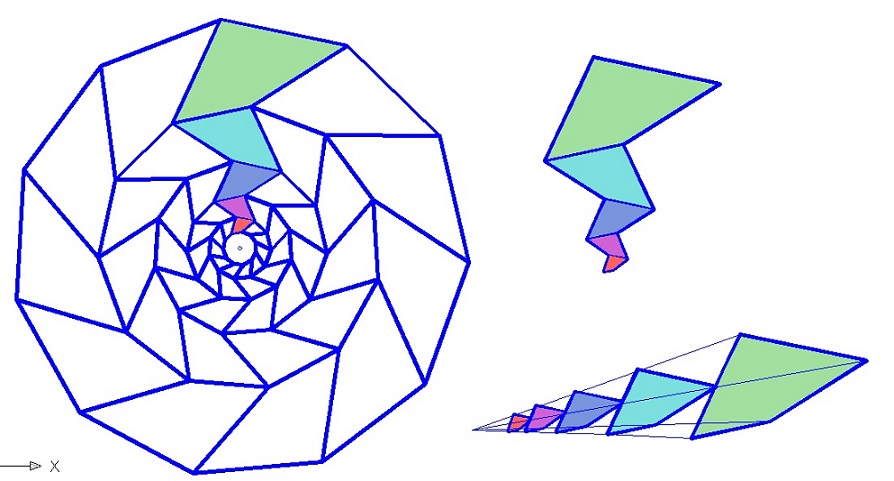
Дополнение от 27.05.2014

 

Укладка круга "золотым паркетом"

 

 

 

 

 

 

 

 

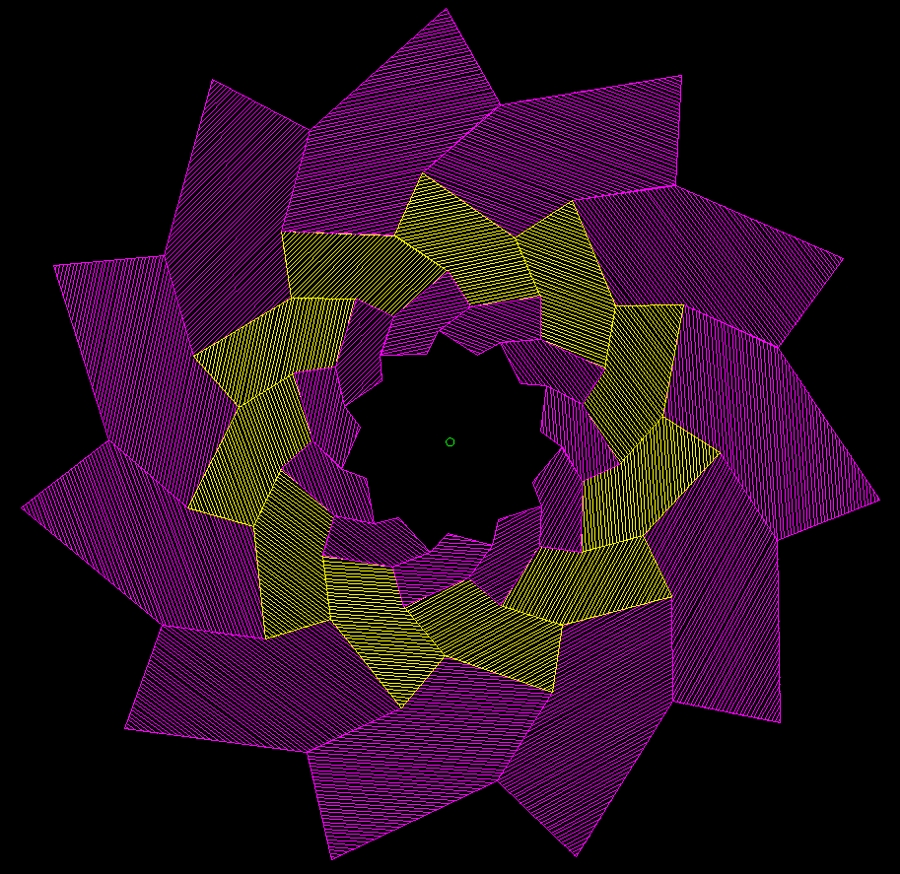
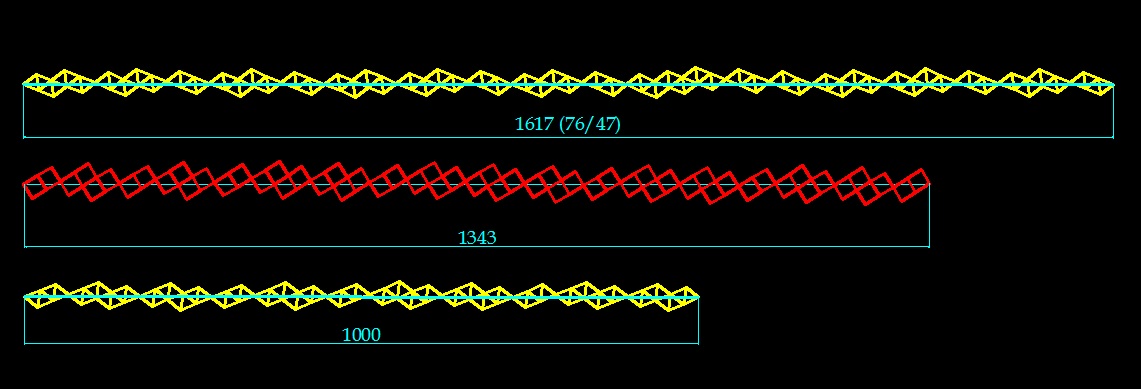
31.05.14. Укладка плиток паркета. Одна сторона плиток равна единице. Другая сторона плиток возрастает по рядe чисел 1, 2, 3, 4, 5, 6, 7 и.т.д. Получается укладка в числах Фибоначчи. Фактически это сектор подсолнуха. 

 

 

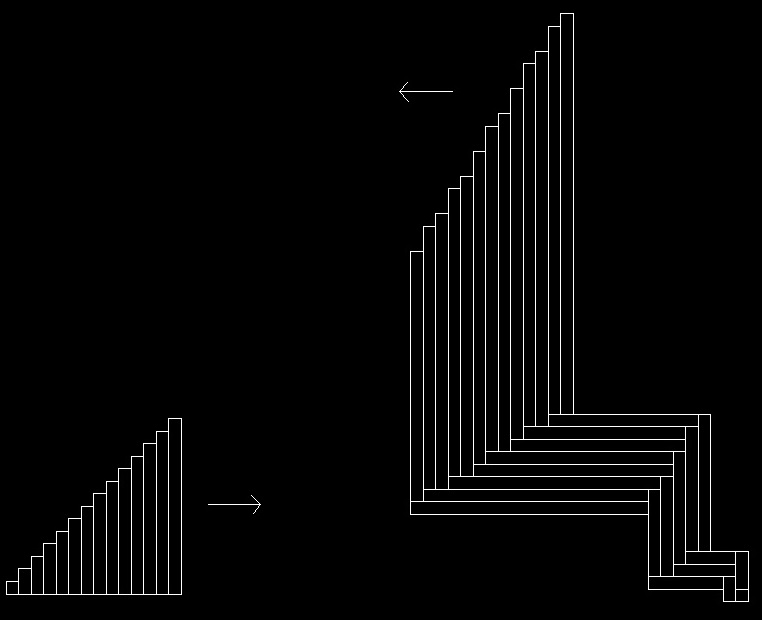
Раскладка семечек, трансформированная из круговой в прямоугольную.

 

 

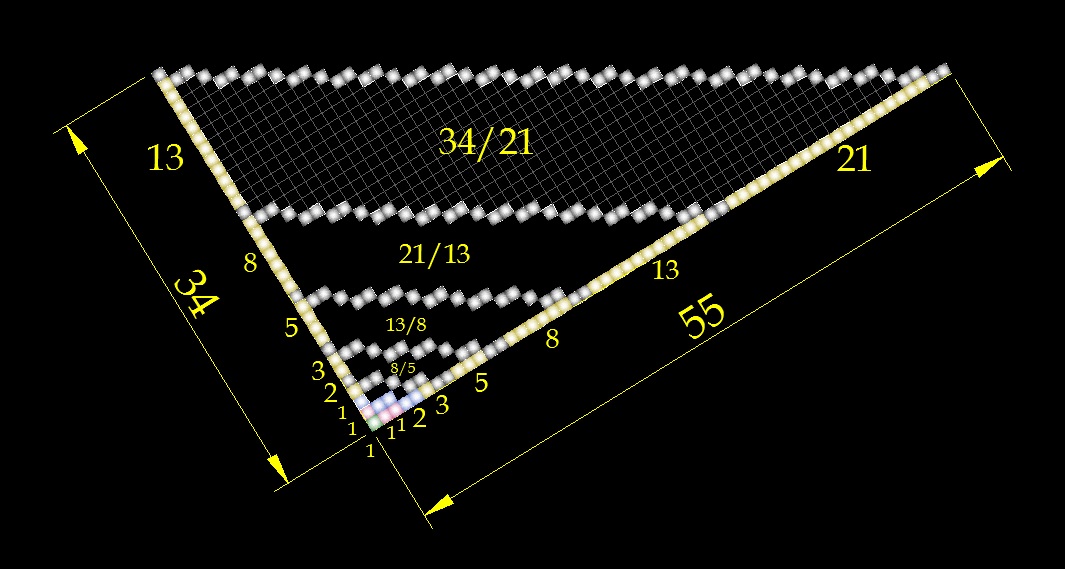
Данная модель позволяет подсчитать количество семян в корзинке.

(55х34)/2 = 935

Каждый новый "виток" увеличивает количество семян в золотой пропорции.

((55х34)/2 - (34х21)/2) / (34х21)/2) = (935-357)/357 = 578/357 = 1,619..

 

 

 

Литература:

 

1. Радзюкевич А.В. Метод геометрического построения спиральных решеток.

 

http://www.a3d.ru/architecture/stat/5

 

2. Щетников А.И. Проблемы филлотаксиса. http://www.nsu.ru/classics/pythagoras/Phyllotaxis.pdf