Продемонстрированы три любопытные формулы-процедуры для вычисления констант золотой пропорции. Они отличаются сверхвысокой скоростью уменьшения ошибок приближения. Одновременно демонстрируются уникальные свойства самого золотого сечения.

Нет ничего быстрее мысли

Золотая константа, которая часто называется также золотым сечением по наименованию исходной геометрической задачи Евклида, определяется иррациональным числом на основе корня пяти Ф = (1+Ö5)/2.

Эта постоянная имеет чисто математический абстрактный смысл и относится к классу целых алгебраических чисел, как корень квадратного уравнения с целыми коэффициентами

x² - x - 1 = 0.

Обратная величина Ф^-1 = Ф - 1 = (-1+Ö5)/2 часто называется нами малой золотой константой, как положительный корень квадратного уравнения x² + x - 1 = 0.

Разложение в цепную (непрерывную) дробь для числа золотого сечения Ф содержит только единицы

,

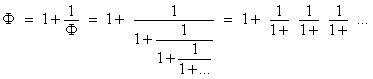что обуславливает самую медленную сходимость по этой форме среди всех других иррациональных чисел.

Прочитать полный текст статьи в формате pdf