Рассмотрено множество триномиальных алгебраических структур как расширение задачи золотого сечения, характеризуемого константой-корнем простейшего квадратного уравнения. Среди них: трином старших степеней, трехчлен с запаздыванием, уравнение k-боначчи в его триадной интерпретации и др. В ходе развития исходной модели образуются новые решения. В общем случае они не имеют ничего общего с золотым сечением, кроме совместной принадлежности к бесконечному множеству алгебраических уравнений.
Изобретал аналогии, которым нет аналогов ...
Золотое сечение (ЗС) имеет тесное отношение к тройственному состоянию вообще и алгебраическим триномам в частности.
Если речь идет о делении целого 1=a+b на две сопредельные части, то имеет место триада {1, a, b}.
Из данных элементов можно составить ограниченное семейство пропорций, а именно:
- деление пополам, 1/a=1/b;
- золотое сечение, 1/b=b/a;
- отсутствие деления так такового.
Наравне с равновеликой дихотомией a=b=0,5 золотое сечение является пропорциональной моделью. Как видно, вполне тривиальной и явственной получаемой. Но одновременно весьма значимой.
За многие столетия появилось много разноплановых описаний золотого сечения.
К сожалению, многие из них больше тяготеют к лженаучным конфигурациям, нежели к фактической картине.
Условно они делятся на три группы:
- слепое благолепие, идущее со времен обожествления золотой пропорции математиком-монахом средневековья Луки Пачоли;
- голословные и малоубедительные утверждения, вроде вольных фантазий о том, что хаос и гармония распределены в отношении ЗС, архитектура «поражена вирусом ЗС» и др.;
- экспериментально-дутые формулировки, когда под ЗС искусственно подгоняется «всё, что ползает и летает», зубы, сердце, пупок, лицо ...
В частности, гипотеза о присутствии ЗС в живых системах обычно выдаётся в качестве некоего догмата.
Без серьезного теоретического обоснования. Как претензия на всеобщность. Когда с помощью различных логических уловок желаемое выдается за действительное.
Изредка, встречаются аргументированные высоко-содержательные материалы.
В основном же преобладают описания, похожие на «отображение соотношений размеров пузырьков в морской пене при движении вилами по воде».
Отметим, что под впечатлением "золотой лихорадки" мы однажды также не удержались от применения золотоносных эпитетов в одной из работ (2008), где обычные исследования корней алгебраических уравнений ошибочно названы «обобщенными ЗС».
Правда, в кавычках. Тем самым всё-таки подчеркивалась условность словосочетания.
Постановка задачи.
Мы не ставим целью глубокое исследование модельных структур и числовых последовательностей в зависимости от вида характеристических алгебраических уравнений и начальных условий.
В большей мере всё это уже изучено в математической литературе.
Наша задача - продемонстрировать, что золотоносный квадратный трехчлен x2-x-1 является всего лишь частным случаем тринома xn-pxr-q и никоим образом не отбрасывает на него тень своей позолоты.
Последний, конечно, более сложен. В общем случае не имеет аналитически вычисляемых корней.
Корни определяются поисковыми вычислительными методами.
Напомним, трином (греч. treis три + nomos член) или трехчлен в математике - алгебраическое выражение, состоящее из трёх одночленов.
В отдельных частных примерах триномы могут иметь решение ЗС. При этом невольно возникает соблазн назвать вещественные корни всех разновидностей тринома «обобщенными золотыми сечениями».
Но в действительности это не верно, алогично и противоречит здравому смыслу. Подобно оптическим иллюзиям (рис. 1).
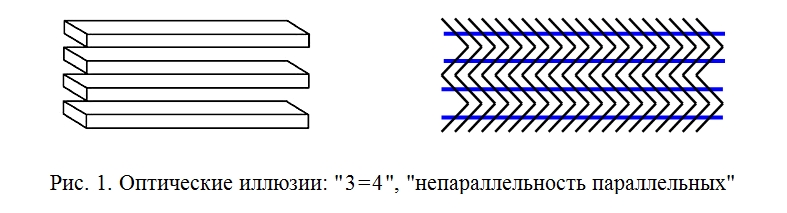
Триномы дают семейство констант, порождаемых выбранным типом алгебраического уравнения. Среди них может быть и ЗС. Ну, и что с того? - Общее алгебраическое уравнение в частном случае также дает модель ЗС. Не называть же его из-за этого обобщенным уравнением ЗС?
После решения задачи пропорционального деления целого на две части процесс моделирования вырождается, а ЗС одновременно становится личным именем математической константы Ф≈1,618.
Этим самым проблематика структурирования ЗС себя исчерпывает.
Константы не обобщаются.
Искусственное навешивание золотых ярлыков себя не оправдывает и несет за собой терминологическую сумятицу и понятийный вздор.
Пути расширения задачи ЗС.
В понятийном аспекте золотоносные термины-эпитеты должны отбрасываться или уходить на задний план, как только мы переходим на структуры, которые в своей основе не содержат константу Ф.
В то же время допустимо говорить о развитии задачи ЗС. Но уже без золотого окраса. Используя отдельные свойства и закономерности исходной задачи, и стремясь продолжить их позитивные тенденции-начала на более сложные объекты.
Расширение задач, родственных с золотым сечением, может осуществляться самыми разнообразными способами: повышением размерности исходной модели, добавлением дополнительных членов, введением варьируемых коэффициентов, заменой целочисленных величин вещественными и др.
Действительно, если посмотреть чуть глубже, то практически «любой алгебраический полином с доминирующим положительным корнем, так или иначе, отражает деление единичного отрезка на две части в определённой пропорции» [1]. Пусть достаточно сложной и трудно интерпретируемой.

