Аннотация

Это великое произведение искусства, завещанное древними греками потомкам, продолжает вызывать у нас интерес, в значительной мере, благодаря своему научному фундаменту.

Изучение такого огромного храма позволяет нам получить представление в отношении ощущений его авторов и способствует пониманию того, каким образом люди думали и ощущали на протяжении этого конкретного исторического периода.

Архитектурные особенности восходят к греческой страсти к наукам, в точной математике:  от простых чисел 2 и 3 с их дихотомией  нечётности и даже к их квадратам - 4 и 9 и от Пифагоровых треугольников, с их сторонами, соотносящимися как  3-4-5, лежащим в основании архитектурной организации разделения помещений. Наука и  искусство едины.

Принимая во внимание этот математический базис, мы можем идентифицировать архитектурный фут как базовую единицу измерения, использованную в Парфеноне и раскрыть процессы осознания и схематизации, которые подведут нас намного ближе к скрытой сути этого шедевра.

 

 

Описание

Эссе содержит ряд мнений, цель которых - содействие процессу повышения критического понимания исторического развития Парфенона, а так же его развития с точки зрения архитектурных форм и материала. Перед тем как начать наше прочтение этого архитектурного организма, однако, позволим себе принять к сведению слова Л. Борсари: "Прежде всего, мы должны решить показать предельное уважение подлинности сохранившихся останков древних произведений искусства и полностью отвергать любые предвзятые мнения и идеи, поднимающиеся от прочтения сотен критических работ. Таким образом, наши умы могут свободно исследовать сами здания и внимать к тому, что они должны сказать, делая то, что они делают: оставаясь тихими "i. Поле для исследования довольно велико и широко. Для того, чтобы двигаться "вперед", мы должны следовать пути, ведущему нас "назад" - cквозь читаемые особенности Парфенона к форме его оригинального дизайна. Для нахождения объединяющего принципа, заложенного за беспорядком видимого, нужно позволить в наших умах свершать операции, которые производили люди, проектировавшие  Парфенон.

Храм - это производное мира, чьи культурные реперные точки существенно отличались от тех, что используем мы. Модели дизайна, правила использования, способы геометрических построений и другие вопросы, конечно, тоже отличались. Несмотря на то, что Парфенон утратил целостность  своего изначального облика, останки его по-прежнему уловимы и позволяют нам провести достоверное исследование его архитектуры. Здание исследовалось уже многим ^i[i]. Во многих эссе, написанных об этом, часто упоминаются скрупулёзность и точность его композиционного построения. Изучая дизайн различных элементов, мы медленно начинаем осознавать комбинации, гармонии и пропорции, применимые к творческим задачам, в соответствии с научными теориями Классической эстетики.

Эти теории могут быть обнаружены в древних источниках классической литературы. Так же они показывают нам параллели между архитектурой и скульптурой.  Витрувий^i[ii], в частности, подробно рассматривает точки соответствия, относящиеся к использованным пропорциональным измерениям; Галлен^iv актуализирует вопрос о модульном принципе в скульптуре, ссылаясь на Поликлета, и говорит, что модуль не происходит от системы измерения, которая приведёт к искусственной комбинации абстракций, а заложен в самой скульптуре.

Эти формулировки привели к искусству Ренессанса, к изучению особенностей пропорций и ритма, которые самостоятельно прилагали в своих поисках совершенной красоты такие мастера, как Леон Баттиста Альберти и Леонардо да Винчи.

 Возвращаясь к Парфенону, среди многих вопросов, относящихся к пропорциональности, возможно, что самый спорный - это единица измерения в дизайне и конструкции храма, которая предположительно лежит в основании его формообразования. Бесчисленное множество изучающих и специалистов по классической архитектуре всё ещё вовлечены в это исследование.

Для Витрувия единица измерения определена путем деления длины наиболее короткой стороны стилобата на установленную цифру 27, если это 4-х колонный (тетрастиль) храм и  на 42, если это 6-ти колонный (гексастиль)^v храм. Однако, в отношении 8-ми колонных (октастиль) храмов - одним из которых является Парфенон -Витрувий информации не даёт. 

В 1787 г., Дж. Стюарт представил исследование, в котором он определил единицу измерения  в 0.30827 метра, посредством деления короткой стороны стилобата на 100 частей^vi.

Чтобы решить туже проблему, другие авторы, такие как А. Паккард^vii, А. Аурес^viii и Ф. К. Пенроуз^ix использовали число 100 и получили аналогичные показатели. Плутарх пишет, что Пантеон, над которым работали Калликрат и Иктин, измеряется 100 футами^x; гекатомпедос, '100 футов', древнее название для целла храма. Используя длину внутреней меры для целла, В. Дорпфельд, снова используя число 100, получает   юнит измерения 0,328^xi. Число 100 было так же использовано В. Б. Динсмуром^xii и А. К. Орландосом^xiii в их исследованиях.

Исследование продолжается и на Парфенон-Конгрессе, состоявшемся в Базеле в 1982 году,  были представлены работы многих авторов на тему единицы измерения Парфенона, со множеством различных толкований и выводов.

Примерно в то же время, С. Стакки^xiv выступил с единицей исследования в 0,305 м, посредством принятия внутренних измерений целлы и делением ее на 100 частей. В более поздних исследованиях, Р. Де Цварте зафиксировал меру в 0,2986м как «ионический фут» и установил, что он тоже наличествует в Парфеноне^xv.

Продвигаясь с нашим исследованием далее и принимая вышесказанное во внимание (в частности, комментарии по поводу параллелей между архитектурой и скульптурой), наш следующий шаг - проверить конические столбцы, используемые в храме: они принадлежат к дорическому ордеру и  характеризуются наличием канелюр. Это полые колонны с элементом, размещенным на ее вершине (капитале), частью которого является эхин в форме подушки. Число, появляющееся в процессе измерения различных элементов (и одного, использованного конструкторами), это мера каждой из 20 канелюр, т. е. 0,298 м, архитектурный фут^xvi.  Это важная и значимая цифра для нашего изначального исследования, поскольку она, в общем, измеряет то, от чего происходят применённые к зданию величины пропорций.

 

 

 

 

Рис. 1. Парфенон: восточный фронт (реконструкция)

 

 

 

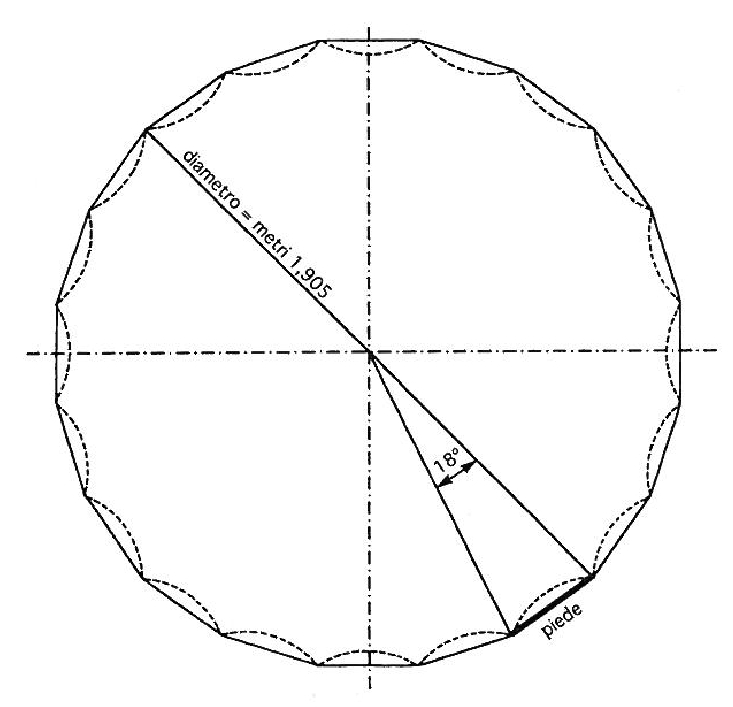
Рис. 2. Парфенон: секция базы колонны

 

 

 

В продолжение нашего исследования, обратим внимание на следующее:

 

1) Использованная единица меры - 0,298 метров,

2) Единица меры может быть найдена в видимой части Парфенона, в каждой из 20 канелюр на  колоннах.

 

Хорошо известно, что одна из особенностей архитектуры Парфенона - это соотношении 4:9, которое регулярно повторяется и просматривается в различных горизонтальных, вертикальных, внутренних и внешних формах.

 

Один из примеров - это горизонтальная конструкция стилобата с высокой ступенью (рис. 3):  соотношение 4:9 между шириной и длиной.

Сперва, мы подметили несколько характеристик по форме колонн; теперь - время взглянуть на их устройство на протяжении периметра, принимая наши измерения во внимание^xvii.

 

 

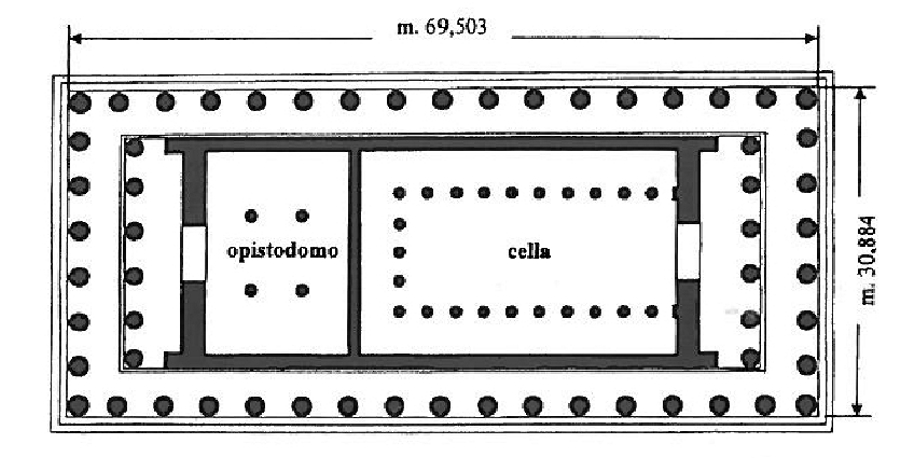
Рис. 3. Парфенон: план пола 69.503 м - 30,884 м

 

 

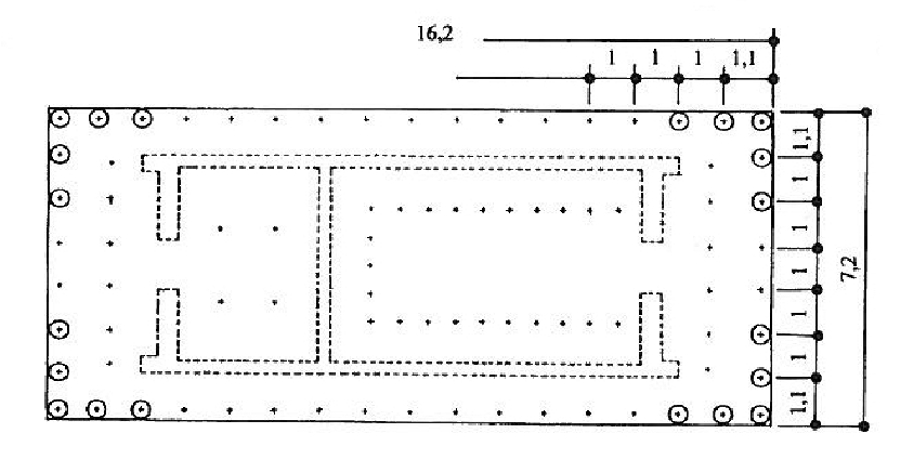
Рис. 4. Парфенон: диаграмма осевого расстояния между колоннами, считаемого от дна их стержней

 

 

Особое внимание следует обратить осевому расстоянию между стержнями колонн (i) и размером стилобата, на которой расположены колонны (размеры которой  30.884 x 69.503 метров). Всего у нас 5 таких расстояний, с добавочными 2-мя (по углам стилобата), и 14 рядовых и 2 угловых расстояния по длинной стороне стилобата (рис. 4). Используя число осевого расстояния между колоннами и соотношение 4:9, мы получаем:

 

7,2: 16,2 = 4 : 9.

 

Наша интерпретация это: объём, сформирован 5-ю расстояниями по оси, + 2 по углам, каждая следующая эквивалентная:

 

1,1 х i

 

таким образом, мы имеем:

 

5 + 1.1 + 1.1 = 7.2.

 

То же самое получаем и для длины

 

14 + 1.1 + 1.1 = 16.2;

 

таким образом, мы вынуждены установить значение осевого расстояния  i.

 

Мы должны совершить ниже следующее действие (учитывая, что ширина стилобата Парфенона составляет 30,884 метра и осевое расстояние между колоннами  i  равно 7,2):

 

30, 884 метра / 7,2=4,29 метра (осевое расстояние  i).

 

Используя те же процедуры, мы можем представить необходимые операции в отношении длины стилобата и получим тот же результат:

 

69.503 метров / 16.2 = 4.29 метров (осевое расстояние i).

 

Если осевое расстояние, измеряющееся как  4.29 м, поделить нашей базовой единицей меры величиной в 0,298 м, то получим 14,4 таких единиц для каждого осевого расстояния (значимое число в свете 7,2, ранее упомянутых). С числом осевых расстояний, являющимся нашим ориентиром, эта процедура позволяет нам отобразить все измерения Парфенона.

Другие значимые числа могут быть найдены из простых соотношений - варьирующихся типов - между измерениями, такими как:

- отношениями между общим числом фронтальных и центральных осевых расстояний между колоннами:  7.2 / 5 = 1.44

 - отношение между шириной и длиной опистодома: 19.040m / 13,220m = 1.44

- отношение между шириной и длиной стилобата и шириной  целлы: 30.884m / 19.065 = 1.62

- отношение между внешней и внутренней длиной секоса (целла + опистодомос) и внутренней длиной целлы: 48.27м / 29.786 = 1.62

Эти, в дальнейшем значимые числа, помогают нам отойти от текущих измерений Парфенона по направлению к измерениям, приведённым в  планах-первоисточниках и пропорциональности в целом.

В следующей секции эти числа помогут нам двигаться от текущих измерений Парфенона к отношениям и измерениям, приведённым в оригинальных планах и пропорциональности в целом.

В текущем разделе мы обращаемся к различным измерениям и отношениям, которые принимают точное значение.  Мы выяснили, что числа 4 - 9 - 7.2 - 14.4 - 1.44 - 16.2 - 1.62,  показывают спектр использованных чисел.

Мы можем видеть, как этот спектр был сформирован, если начнём с простых чисел 2 и 3 в различных их комбинациях:

 

2 / 3

2² / 3² = 4 / 9

2² x 3² = 36 ↔ 72 ↔ 7.2 ↔ 14.4 ↔ 1.44 ↔ 2.88 ↔ 5.76 ↔ 57.6

2³ x 3³ = 64 ↔ 32 ↔ 3.2

3² x 3² = 81 ↔ 162 ↔ 16.2 ↔ 1.62

7.2 / 16.2 = 4 / 9

 

Числа 100 и 192 (64 х 3) так же использованы. Эта группа чисел устанавливает арифметический спектр, использованный в архитектуре храма. Посредством разделения и умножения этих чисел мы можем найти другие числа, присутствующие в Парфеноне. Это содержит в себе:

 

4.32 = 1.44 x 3;

 

2.43 (перестановки числа 4,32) ^xviii;

 

8,1 и 1,8.

 

Используя измерения, найденные в основании канелюры колонны (0,298 метра) и числа, полученные из исследований, мы можем найти эти числа в значениях и отношениях между различными архитектурными элементами, горизонтальные ли они, вертикальные, внешние или внутренние. Ранее, мы упоминали об архитектуре и более близких отношениях, которые связывают её язык с языком скульптуры. В поддержку этой концепции, мы уверены, что Р.Карпентер выражает это обстоятельно в своей известной работе. Он говорит, что каждый рассматривающий остатки древнегреческого храма без восприятия сходств между двумя искусствами, благодаря которым общее впечатление от множества сотен разрозненных частей было смешано вместе в монолитное целое так, если бы это была скульптура, терпит провал в попытках понять истинный уровень достижений греческой архитектуры^xix.

Анализ, который мы представляем, ведёт нас к пониманию величин, соотношений между величинами и пропорциями, которые определяют расположение различных компонентов: мы можем видеть связи и частичные совпадения и логически вывести некоторые правила. Через соотношение, которое появляется в различных местах, соотношение 4 : 9, мы нашли самостоятельно в одной из 'категорий' Витрувия, т. е. симметрии (рис. 5). Здесь есть соотношение между шириной и длиной Парфенона, которое древние называли симметрией. Несмотря на то, что две эти величины не являются равными, тем не менее они - производное от общей единицы измерения.

 

 

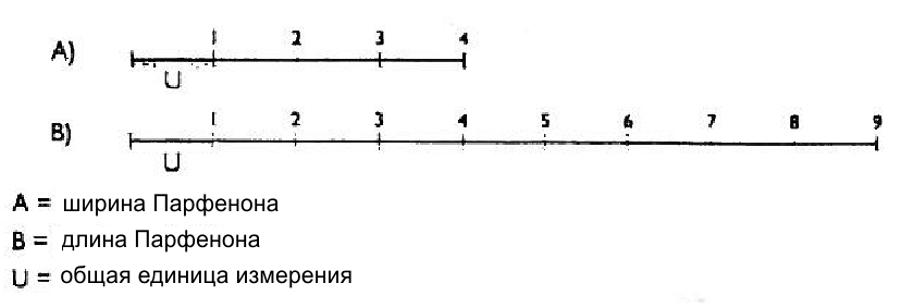
Рис. 5. Симметрия: сегменты А и В делятся в соотношении 4 : 9.

 

 

Используя общую единицу измерения U  на передней части Парфенона, мы находим:

 

 

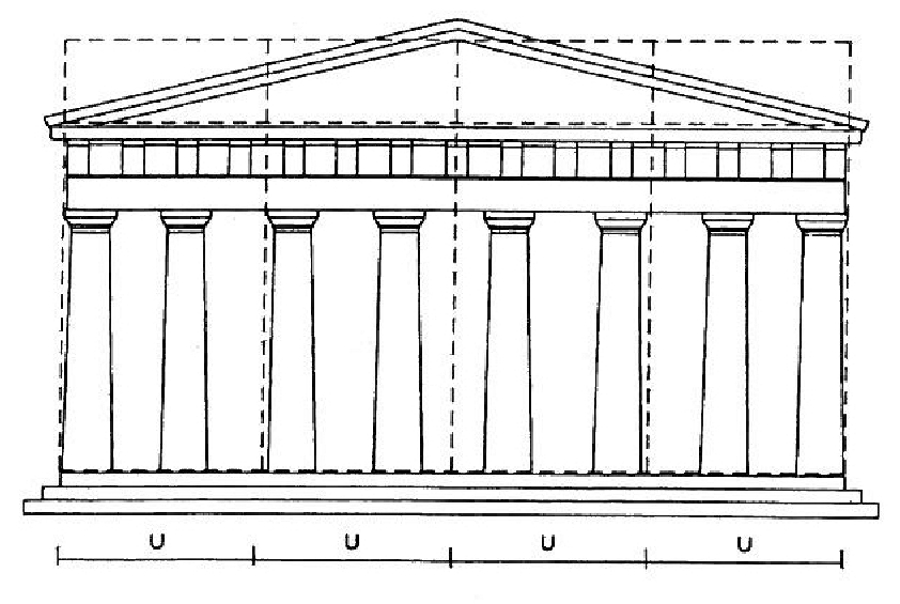
Рис. 6. Парфенон: фронтальный вид с диаграммой общей единицы измерения.

 

 Из предшествующего рисунка мы заключили:

 

 

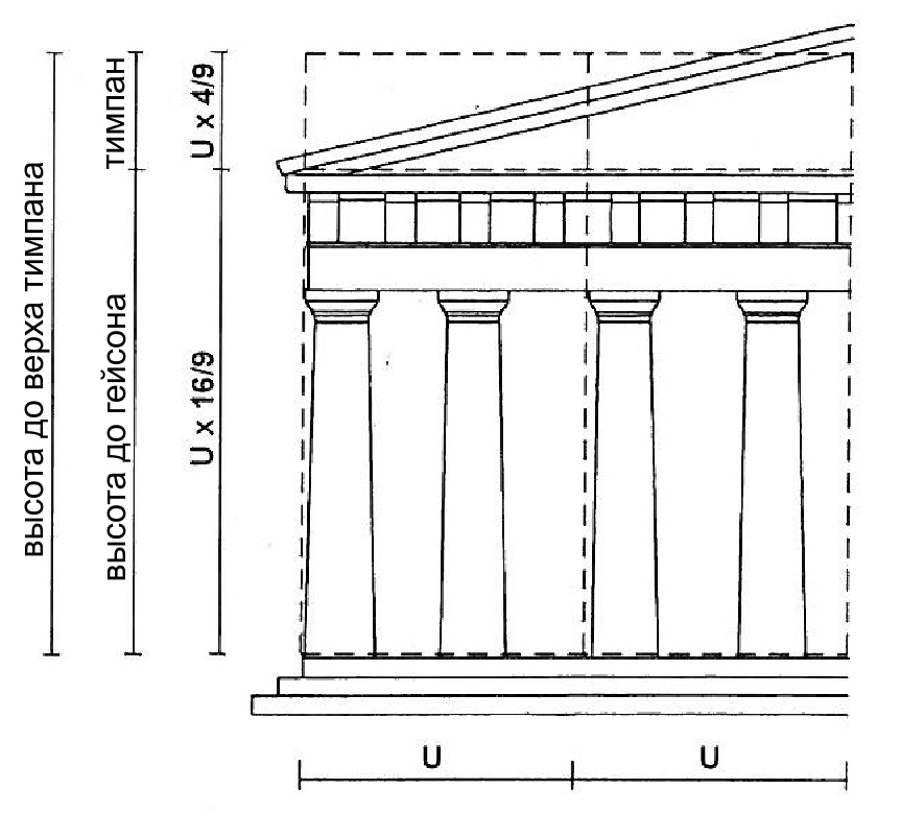
Рис. 7. Парфенон: диаграмма общей меры U на вертикальном плане, показывающем тоже  соотношение 4 : 9 , найденное на плане пола.

 

 

Продвигаясь далее к соотношению 4 : 9, мы можем разделить общую меру U на 9 частей:

 

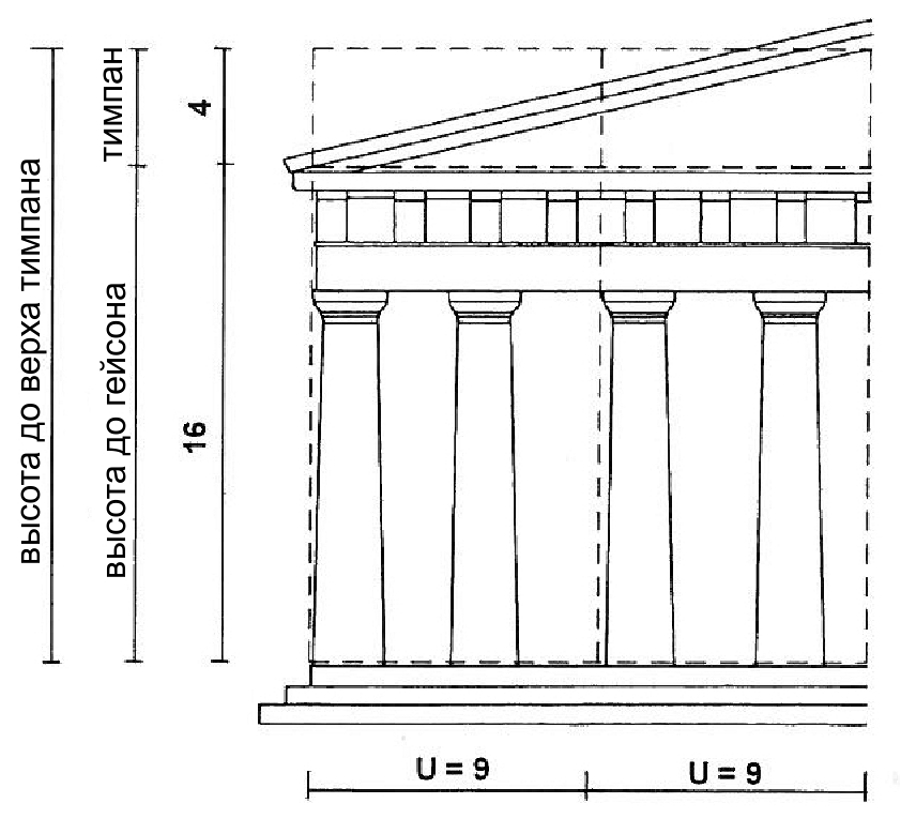
Рис. 8. Парфенон: диаграмма общей меры U  на вертикальном плане, с подразделениями.

 

При помощи этих последних вычислений мы достигли центрального узла нашего исследования: информация в отношении основных пропорций относится к архитектурной композиции Парфенона. Эти пропорции формируют численный деления через гармонию каждой части с другими частями и со зданием в целом (рис. 9).

В отношении к горизонтальным измерениям, высоты следующих выразительны: колонны, архитрав (эпистиль), фриз (триглиф-метопа), карниз (гейсон) и тимпан, другими словами, высота от стилобата к вершине; мы должны помнить и осевые расстояния между колоннами, потому что в сумме они очень важны для формулы в целом. Исследование ведёт нас к набору разделений (перегородок), где каждый архитектурный компонент в завершённой гармонии: эти разделения лежат в основании оригинальных планов и являются канвой, по которой осуществляется формообразование.

 

 

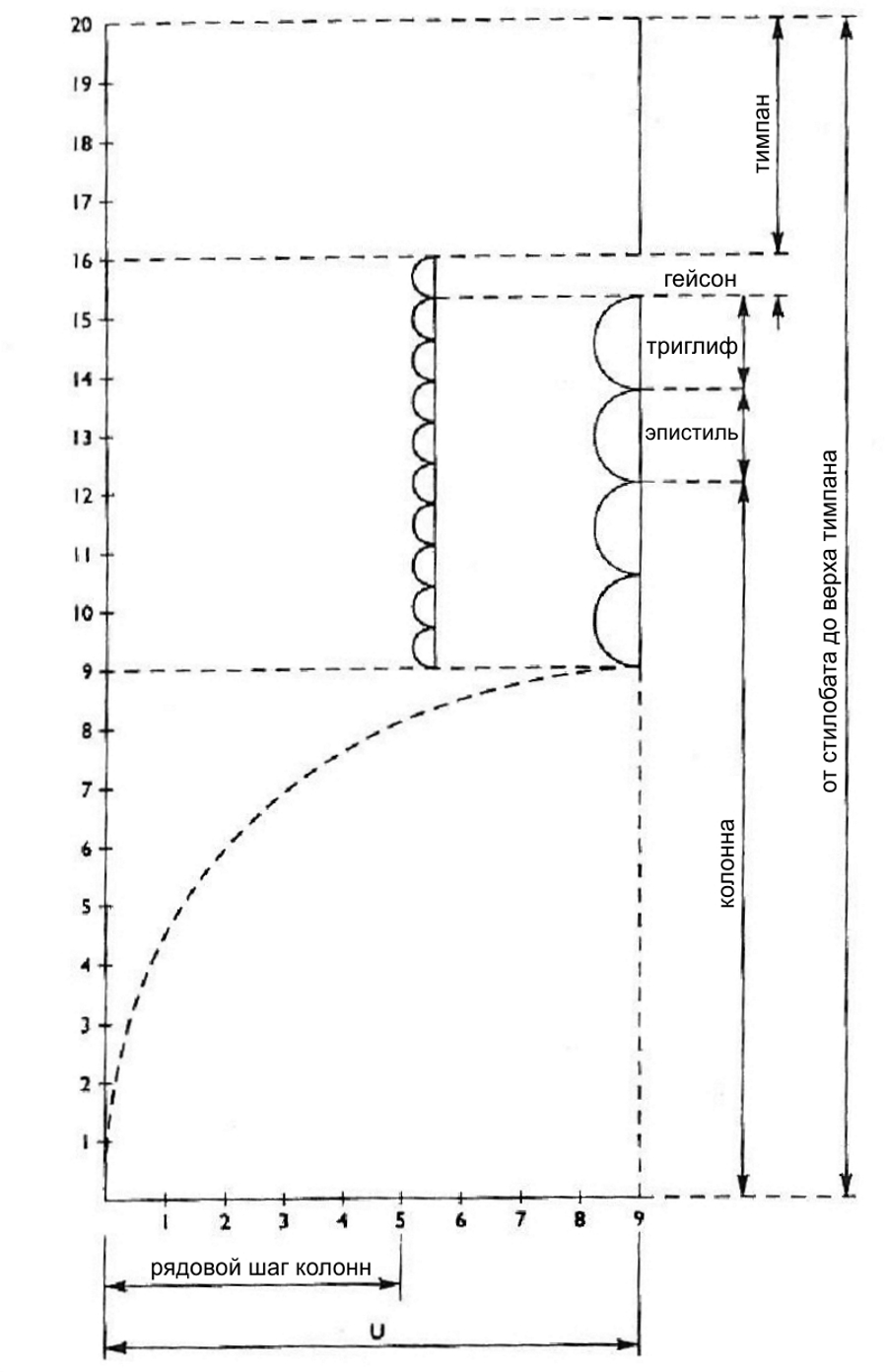
Рис. 9. Парфенон: диаграмма трёх разделений. Отношения сформированы между горизонтальными и вертикальными элементами

 

С этим разделением архитектурных компонентов мы завершили логическую организацию (методологию) нашего исследования, которая развивается вокруг 4-х ключевых пунктов:

1)  Архитектурная единица измерения -  0,298м;

2)  Единица измерения прослеживается в архитектуре Парфенона, в колоннаде;

3)  Спектр чисел, произошедший от первичных чисел 2 и 3, использован в его архитектуре;

4)  Использованные соотношения определяют архитектурную композицию.

 

Если мы примем измерения, соответствующие нашей базовой единице (0,298 метров - архитектурный фут) и его развития как средства применения простых чисел 2 и 3, в горизонтальных и вертикальных величинах, и пропорциях, и с разделением, связанным с этими вычислениями, мы можем вывести основополагающие конструктивные элементы, проведя серию операций.

Применяя разделения к архитектурным элементам, мы получаем:

 

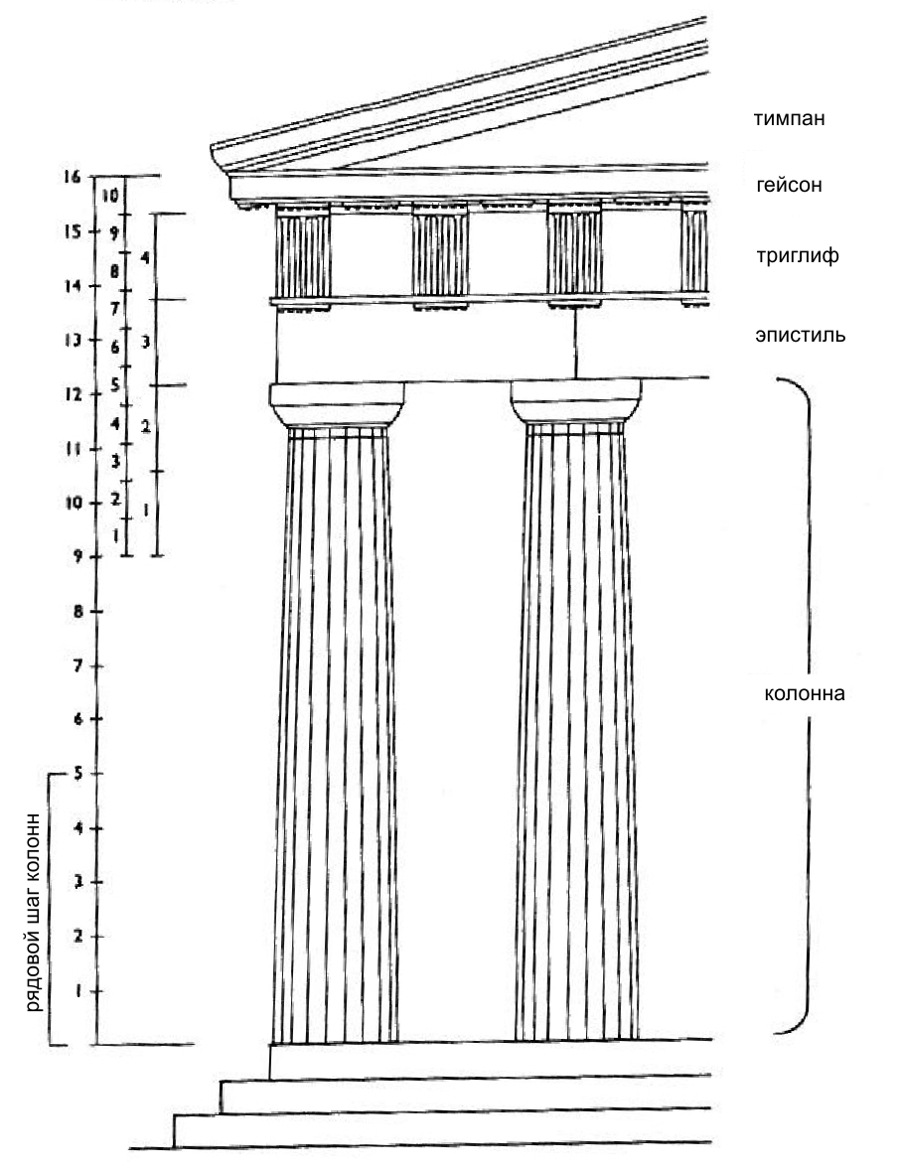
Рис. 10. Парфенон: архитектурные элементы с вертикальным разделением.

 

 

Из Таблицы 1 мы можем увидеть, что целые числа в  спектре (192 - 162 - 100 - 72 - 64) устанавливают «краеугольные камни» конструкции (рис. 11).

Принимая во внимание, что ширина и длина стилобата имеет соотношение 4 : 9, мы можем заменить их этими числами (рис. 12).

Также мы можем провести треугольники с «Пифагорейской» триадой 3-4-5^xvii; что позволяет нам подтвердить присутствие прямых углов без использования любых специальных инструментов.

Определение основных мер в терминах целых чисел, относящихся к первоначальному спектру,  должно было происходить с лёгкостью, уже только потому, что упростилось взаимодействие между различными ремесленниками. Используя эти измерения, мы можем установить с точностью геометрическое соответствие между внешним периметром и секосом; и, если мы продолжим двигаться вдоль  прямых и диагональных линий, мы завершим стороны стилобата;  затем с использованием «Пифагорейских» 3-4-5 треугольников мы подтвердим длины сторон и то, что углы прямые. С дальнейшим измерением внутренней длины целлы как 100 футов, посредством геометрии и с помощью линеек и компасов, мы можем вывести другие значимые измерения и, принимая во внимание, требования всей композиции в целом, мы соразмеряем небольшие пространства архитектурных компонентов. Это диалог между арифметикой, геометрией и композицией.

 

 

Таблица 1: Сопоставление расчетных размеров с данными по Орландосу (в скобках).

 

Высота колонн	10,427	(10,430)
Триглиф	1,352	(1,350)
Эпистиль	1,352	(1,351)
Гейсон	0,601	(0,600)
Высота от стилобата до гейсона (высота ордера)	13,731	(13,730)
Высота тимпана	3,432	(3,428)
От стилобата до верха тимпана	17,164	(17,16)
Ширина стилобата	30,895	(30,884)
Длина стилобата	69,514	(69,503)
Внешняя длина секоса (целла + опистодом), 162 фута	48,276	(48,270)
Полное угловое расстояние между колоннами на внешней стороне секоса, 192 фута	57,216	(57,236)
Внешняя ширина целлы на высоте фриза, 72 фута	21,456	(21,440)
Внутренняя длина целлы, 100 футов	29,800	(29,786)
Внутренняя ширина целлы, 64 фута	19,072	(19,065)
Внутренняя длина опистодома, 44 4/9 фута	13,244	(13,220)
Внутрення глубина опистодома, 64 фута	19,072	(19,040)
Сумма 5-ти осевых расстояний между колоннами, 72 фута	21,456	(21,474)

 

 

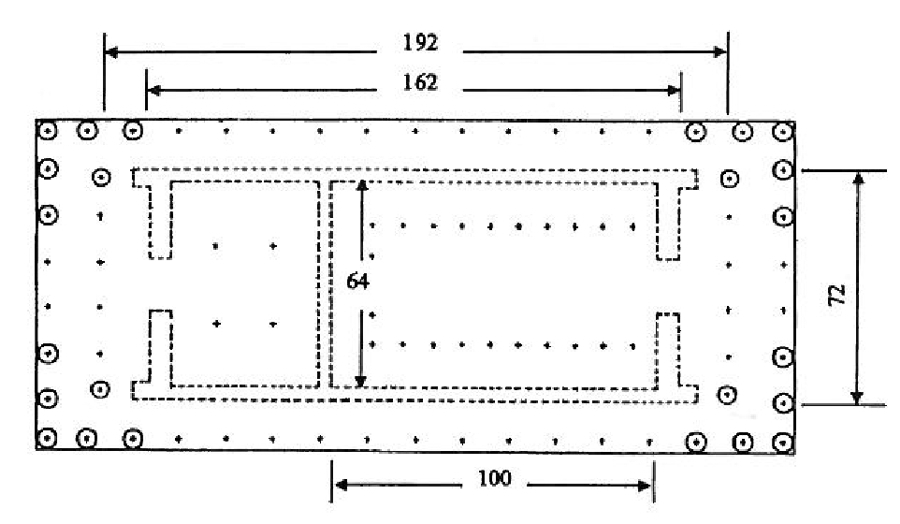
Рис.11. Измерения Парфенона выраженные в величинах фута.

 

 

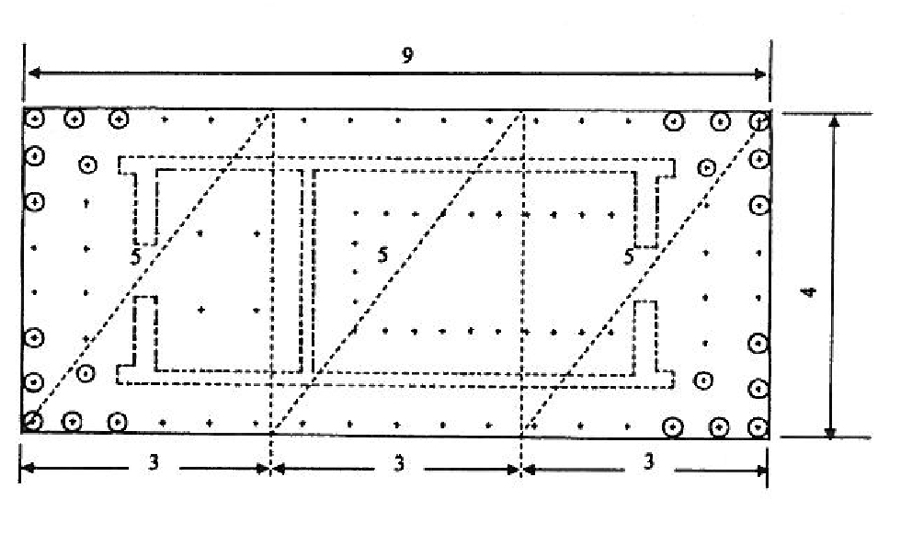
Рис.12. Измерения Парфенона выраженные с помощью построения пифагорейских треугольников.

Нельзя отрицать, что Парфенон - экстраординарный комплекс. Однако, это не только сложность, происходящая от коллективного воображения, от клише, происходящих из риторики сверх-энтузиастов, или идея бесконечных чисел, или от мистических 'чисел'; это сложность, произошедшая от гениальности его дизайна и разделений. Пропорции и соответствия, в различных комбинациях, выделены в нескольких местах, и особенный числовой спектр определяет динамику (движения), созданные в процессе его проектирования.

Работа архитектора Парфенона (начальника и надсмотрщика за строительством) - это совместительство деятельности архитектора и скульптора, преимущественно, была поручена Фидию ^xxi

Довольно необычное задание для скульптора, которое ведущий художник представил с непревзойдённым мастерством.

 

 

ИТОГОВЫЕ РЕМАРКИ

 

Мы идентифицировали архитектурную меру у основания канеллюры колонны, т. е. 0,298 м. -   единицу измерения, использованную для того, чтобы получить результаты нашего исследования. Однако мы находим число 1 в колоннах, в то время как число 20 задано нам  периметром колонн (20 канелюр).

Из обобщения оригинальных измерений мы получаем дальнейшие целые числа (192 - 162 - 100 - 72 - 64); другие измерения также возрастают, такие как осевое расстояние между колоннами (14,4 фута), в то же время мы получаем  общую высоту в 57,6 футов.

Мы упомянули спектр чисел 7.2 - 16.2 - 1.44 - 1.62, и другие, выраженные в десятичной форме; всё это может быть найдено в гармониях, пропорциях, вариациях и подстановках в композиции храма, как трактат по прикладной десятичной арифметики Классического периода.

 

Посему, мы можем вывести положение, что Парфенон - математическое пространство классическое и современное одновременно, вводит в силу модель архитектурного разделения и взаимоотношения между формами, происходящими от наивысших и наиболее усовершенствованных артистических способностей как необходимый элемент в контексте  города Афины.

 

 

ПРИМЕЧАНИЯ

 

i L. Borsari, Il Foro Romano ('The Roman Forum'), Rome 1899; Giuliani/Verduchi 1987, 11.

 

ii One of the most valuable studies, with scale drawings and metrical measurements, is AK Orlandos' 1977-78 publication.

 

iii Vitruvius, De Architectura 3.1.65: 'The parts of temples must have, with a similar method to that of the ancient painters and sculptors, perfect correspondence and concordance between the measurements of the individual parts and between each part and the total of the whole'. Cfr. Arias 1964, 47.

 

iv Galen, de placita Hippocratis et Platonis 5.3: '[Chrysippus] on the other hand maintains that beauty is not found in the symmetry of the elements but in that of the parts, of the finger in relation to each other finger and of all the fingers in relation to the metacarpal and the carpal, and of these when compared with the forearm, and of the forearm compared with the arm; and of all these in relation to the whole, according to what is written in the Canon of Polycletus'. Cfr. Arias 1964, 46.

 

v Vitruvius, De Architectura 4.3; Stucchi 1983, 21.

 

vi Stuart 1787, 8.

 

vii Obtained the unit of measurement 0.3085: Aurès 1867, 12.

 

viii Obtained the unit of measurement 0.3089: Aurès 1867, 13.

 

ix Obtained the unit of measurement 0.3088: Penrose 1888, 7.

 

x Plutarch, Vita di Pericle ('Life of Pericles') 13.7; Magnino 2006, 49.

xi Dörpfeld 1890, 172.

 

xii Obtained the unit of measurement 0.32685: Dinsmoor 1950, 161.

 

xiii Obtained the unit of measurement 0.32878: Orlandos 1977-1978, 699.

 

xiv Stucchi 1983, 25.

 

xv De Zwarte 1994, 142-143; 2002, 14-18.

 

xvi Brigo 1999, 63-67, 104

 

xvii Orlandos 1977-1978

 

xvii Through the fraction ¾, the number 4.32 gives us: 4.32 x ¾ = 3.24 and 3.24 x ¾ = 2.43.

 

ixx Carpenter 1979, 85 (Italian version).

 

xx This was the first right-angled triangle to be expressed using whole numbers: Lidonnici 1935, 436; Tiberi 1964, 119; Frajese 1970, 146; Vitruvius, De Arch. 9: On Pythagoras' invention to form a right-angled set square.

 

xxi Plutarch, Vita di Pericle (Life of Pericles) 13.6; Magnino 2006, 47-49

 

 

 

БИБЛИОГРАФИЯ:

 

Ameling, W. 1985, Plutarch, Perikles 12-14, Historia 34, 47-63.

 

Arias, P.E. 1964, Policleto, Florence.

 

Aurès, A. 1867, Etude sur les dimensions du Parthénon, Nimes.

 

Berger, E. (ed.) 1984, Parthenon-Kongeress Basel 1982, Mainz.

 

Brigo, R. 1999, Partenone - tre partiture, Verona.

 

Carpenter, Rh. 1979, Gli architetti del Partenone, Turin (Italian translation of the original).

 

Dinsmoor, W.B. 1950, The Architecture of Ancient Greece, London.

 

Dörpfeld, W. 1890, 'Metrologische Beitrage', AM 15, 167-187.

 

Frajese, A. / Maccioni L. (ed.) 1970, Euclide, Gli Elementi, Turin.

 

Franciosi, F. 1977, L'irrazionalità della matematica greca antica, Rome.

 

Giuliani, C.F. / Verduchi, P. 1987, L'area centrale del Foro Romano, Florence.

 

Lidonnici, A. 1935, Pitagora e Pitagorismo (Enciclopedia Italiana di Scienze, Lettere ed Arti 27), Rome.

 

Magnino, D. (ed.) 2006, Plutarco - Vite, 2, Turin.

 

Orlandos, A.K. 1977-1978, He Architektonike tou Parthenonos, 1-2, Athens.

 

Penrose, F.C. 1888, An Investigation of the Principles of Athenian Architecture, London.

 

Stuart, J. 1787, Antiquities of Athens, London.

 

Stucchi, S. 1983, La corrispondenza metrica del cosidetto "piede partenonico" (Accademia Nazionale dei Lincei - Rendiconti 379,8), Rome.

 

Tiberi, C. 1964, Mnesicle, l'architetto dei Propilei, Rome.

 

Zwarte, R. De 1994, 'Der ionische Fuss und das Verhältnis der römischen, ionischen und attischen Fussmasse zueinander', BABesch 69, 115-143.

 

Zwarte, R de 2002, 'Evidence of the so-called Golden Section in Archaic South Italy: the Hera Temple I ('Basilica') at Paestum. With an addendum on the Parthenon at Athens', BABesch 77, 9-18.

 

 

 

 

Оригинал статьи на итальянском языке