Всё определяется пропорциями:
искусство, разведка, любовь, политика...
К-ф «Семнадцать мгновений весны»
В научной и популярной литературе можно немало прочесть о золотом сечении - редчайшем, необычном построении, с красивыми рекуррентными формулами.
Оно, конечно, притягивает внимание, как и всякий феномен. Но часто возникает и некоторое предубеждение, которое настораживает и даже отталкивает.
Противоестественной и явно надуманной представляется известная фетишизация и обожествление золотой пропорции. Явление, которое больше порождено состоянием эйфории нескольких исследователей, чем фактической картинкой математических реалий.
А они таковы, что содержат такое огромное количество необыкновенных конструкций, что для их систематики не хватит не только названий благородных металлов, но и никаких таблиц химических элементов или драгоценных камней.
Тем не менее, термин "золотая пропорция" прижился. Пусть таковым и остаётся.
Что касается исключительности золотого сечения, то здесь не всё так очевидно и требует освобождения от традиционных методологических ограничений. С более широким изучением сходных структур и подключением обновлённых методов мышления.
Безальтернативная конструкция. Остановимся на традиционном геометрическом представлении математического сечения. Будем оперировать только тремя величинами-отрезками прямой и двух её частей {1, a, b}, без каких-либо дополнительных операций над ними: суммы, разности, умножения на вещественное число и т.п.
Приложив минимум мыслительных усилий, легко разобраться, что из такого набора (целого и его двух слагаемых) просто невозможно создать иной пропорции, кроме золотой!
Если конечно, ещё раз подчеркнём (!), не прибегать к конструктивным дополнительным образованиям типа вычитания частей b-a, их умножения на весовые коэффициенты и прочие вычислительные премудрости. То есть в данном случае имеем три объекта {1, a, b}, связанные формулой 1=a+b, и одну-единственную (!) пропорцию
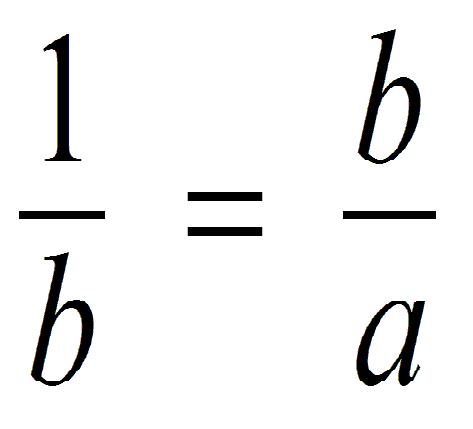
Так, две спички можно положить крестиком, параллельно, буквой "г", в одну линию.
Здесь же, как в трёх соснах {1, a, b}, ни одного дополнительного варианта!
Никакой альтернативы! Не считая тождественных модификаций, свойственных любой пропорции, как-то: обращения, перестановки членов и проч.
Так, в чём же тогда божественность-золотистость? - Неужели в том, чтобы составить очевидное и единственно мыслимое возможное равенство отношений (1)...
Примерно как в одном сказочном эпизоде, когда козлик вынимал из мешка и бросал обратно одну и ту же волчью голову, всё больше пугая тем самым своих врагов.
Не нужно быть семи пядей во лбу, чтобы из множества {1, a, b} составить пропорцию (1), в коих ещё древнегреческие учёные были большие мастера.
Данная пропорция, несомненно, являлась для них проходной задачкой. Весь смысл состоял не в образовании самоочевидной пропорции (целое - к большему как оно - к меньшему) или подборе некоторого приближённого решения. Что довольно-таки легко, в тех же отношениях целых чисел.
Полный текст сьатьи в формате pdf

